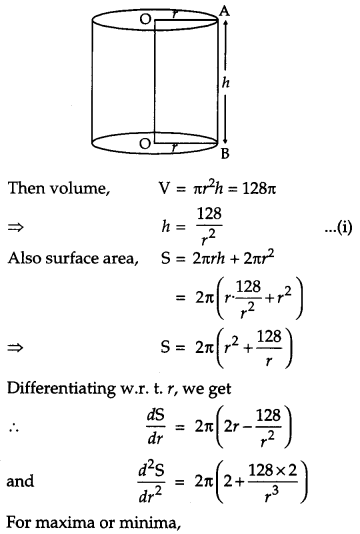CBSE Previous Year Question Papers Class 12 Maths 2014 Delhi
Time allowed: 3 hours
Maximum marks : 100
General Instructions:
- All questions are compulsory.
- The question paper consists of 29 questions divided into four sections A, B, C and D. Section A comprises of 4 questions of one mark each, Section B comprises of 8 questions of two marks each, Section C comprises of 11 questions of four marks each and Section D comprises of 6 questions of six marks each.
- All questions in Section A are to be answered in one word, one sentence or as per the exact requirement of the question.
- There is no overall choice. However, internal choice has been provided in 1 question of Section A, 3 questions of Section B, 3 questions of Section C and 3 questions of Section D. You have to attempt only one of the alternatives in all such questions.
- Use of calculators is not permitted. You may ask for logarithmic tables, if required.
**Answer is not given due to the change in present syllabus
CBSE Previous Year Question Papers Class 12 Maths 2014 Delhi Set I
Section – A
Question 1.
Let * be binary operation, on the set of all non-zero real numbers, given by a * b = \(\frac{a b}{5}\) for all a, b ϵ R – {0}. Find the value of x, given that 2 * (x * 5) = 10.** [1]
Question 2.
If \(\sin \left(\sin ^{-1} \frac{1}{5}+\cos ^{-1} x\right)\)= 1, then find the value of x. [1]
Solution:
Given,
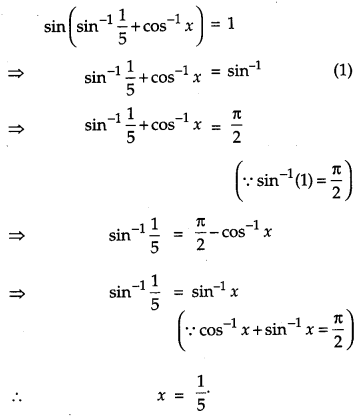
Question 3.
If \(2\left[\begin{array}{ll}{3} & {4} \\ {5} & {x}\end{array}\right]+\left[\begin{array}{ll}{1} & {y} \\ {0} & {1}\end{array}\right]=\left[\begin{array}{cc}{7} & {0} \\ {10} & {5}\end{array}\right]\), find (x – y). [1]
Solution:
Given,
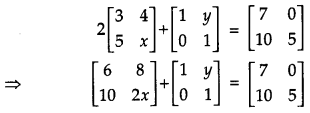
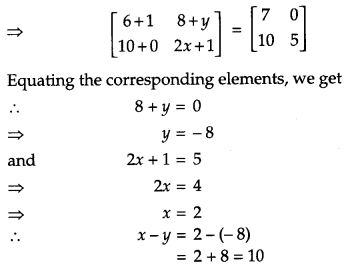
Question 4.
Solve the following matrix equation for [1]
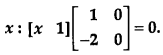
Solution:
Given,
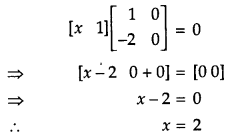
Question 5.
If \(\left|\begin{array}{cc}{2 x} & {5} \\ {8} & {x}\end{array}\right|=\left|\begin{array}{rr}{6} & {-2} \\ {7} & {3}\end{array}\right|\), write the value of x. [1]
Solution:
Given,
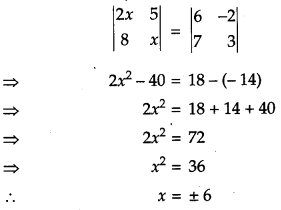
Question 6.
Write the antiderivative of \(\left(3 \sqrt{x}+\frac{1}{\sqrt{x}}\right)\). [1]
Solution:
The antiderivative of \(\left(3 \sqrt{x}+\frac{1}{\sqrt{x}}\right)\)
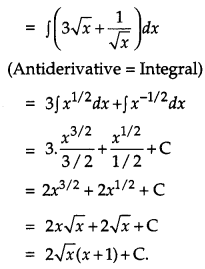
Question 7.
Evaluate: [1]
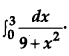
Solution:
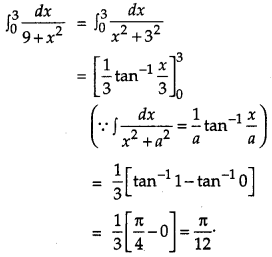
Question 8.
Find the projection of the vector \(\hat{i}+3 \hat{j}+7 \hat{k}\) on the vector \(2 \hat{i}-3 \hat{j}+6 \hat{k}\). [1]
Solution:
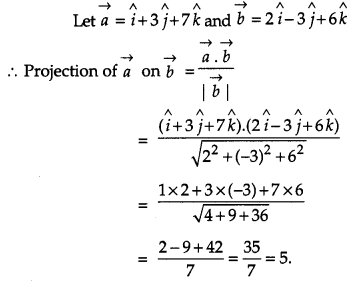
Question 9.
If \(\vec{a} \text { and } \vec{b}\) are two unit vectors such that \(\vec{a}+\vec{b}\) is also a unit vector, then find the angle between \(\vec{a} \text { and } \vec{b}\). [1]
Solution:
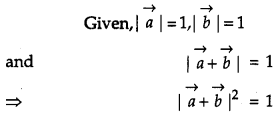
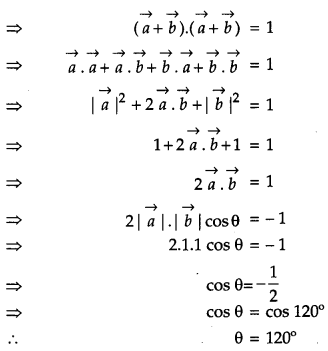
Question 10.
Write the vector equation of the plane, passing through the point (a, b, c) and parallel to the plane \(\vec{r} \cdot(\hat{i}+\hat{j}+\hat{k})=2\). [1]
Solution:
The given plane is

Section – B
Question 11.
Let A = {1, 2 , 3, ………., 9} and R be relation in A × A defined by (a, b) R (c, d) if a + d = b + c for (a, b), (c, d) in A × A. Prove that R is an equivalence relation. Also obtain the equivalence class [(2, 5)]. [4]
Solution:
Here, A = {1, 2, 3, ………, 9} and R is a relation on A × A defined by
(a, b) R (c, d) ⇔ a + d = b + c ∀ a, b, c, d ϵ A
(i ∀(a, b) ϵ A × A
a + b = b + a
⇒ (a, b) R (a, b) ∀ (a, b) ϵ A × A
⇒ R is reflexive on A.
(ii) Let (a, b) R (c, d)
⇒ a + d = b + c
⇒ b + c = a + d
⇒ c + b = d + a
⇒ (c, d) R (a, b)
⇒ R is symmetric on A.
(iii) Let (a, b) R (c, d) and (c, d) R (e,f)
⇒ a + d = b + c and c + f = d + e
⇒ (a + d) + (c + f) = (b + c) + (d + e)
⇒ a + f = b + e
⇒ (a, b) R (e, f)
⇒ R is transitive on A.
Hence R is an equivalence relation on A.
Also equivalence class [(2, 5)]
= {(a, b) ϵ A × A | (2, 5) R (a, b)}
= {(a, b) ϵ A × A | 2 + b = 5 + a}
= {(a, b) ϵ A × A | b = a + 3}
= {(a, a+ 3) | a ϵ A).
Question 12.
Prove that [4]
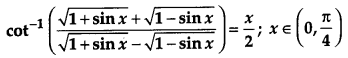
Solution:
L. H. S.
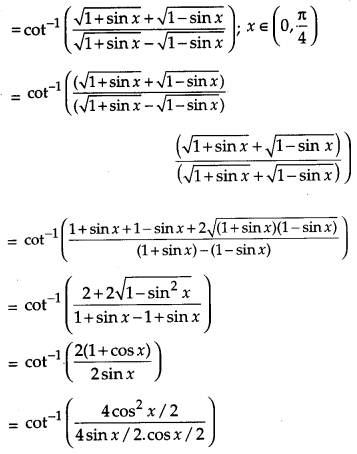
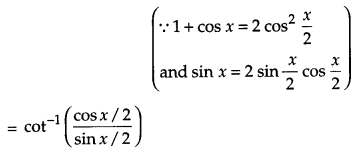
![]()
OR
Prove that:
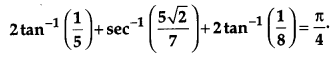
Solution:
L. H. S.
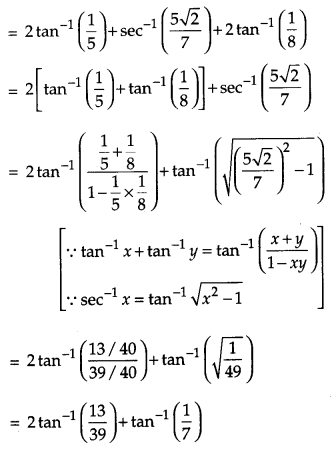
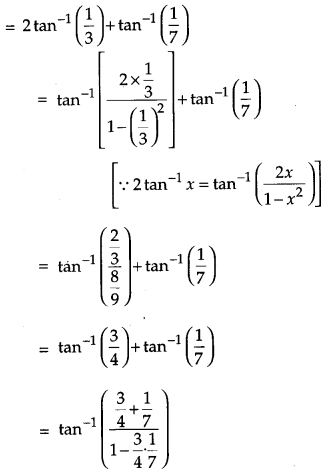
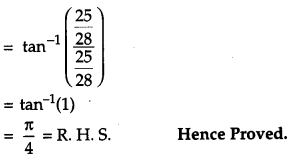
Question 13.
Using properties of determinants, prove that [4]
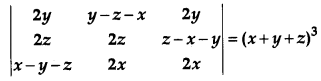
Solution:
Taking L. H. S.

Question 14.
Differentiate \(\tan ^{-1}\left(\frac{\sqrt{1-x^{2}}}{x}\right)\) with respect to \(\cos ^{-1}(2 x \sqrt{1-x^{2}})\), when x ≠ 0. [4]
Solution:
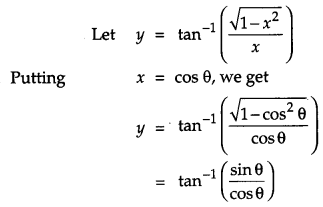

Question 15.
If y = xx, prove that [4]

Solution:
Given, y = xx

Question 16.
Find the intervals in which the function f(x) = 3x4 – 4x3 – 12x2 + 5 is [4]
(a) strictly increasing
(b) strictly decreasing
Solution:
Here
f(x) = 3x4 – 4x3 – 12x2 + 5
⇒ f'(x) = 12x3 – 12x2 – 24x
= 12x (x2 – x – 2)
= 12x [x2 – 2x + x – 2]
= 12x[x(x – 2) + 1(x – 2)]
= 12x (x + 1) (x – 2)

OR
Find the equations of the tangent and normal to the curve x = a sin3 θ and y = a cos3θ at θ = \(\frac{\pi}{4}\).
Solution:
The given curve is x = a sin3 θ; y = a cos3 θ …(i)

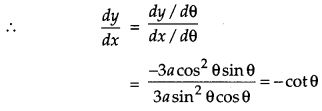
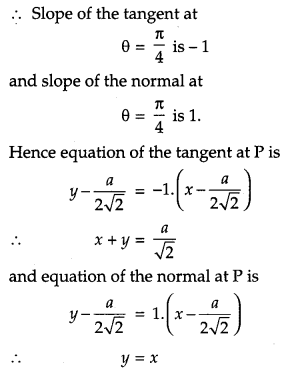
Question 17.
Evaluate: [4]
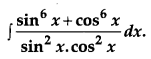
Solution:
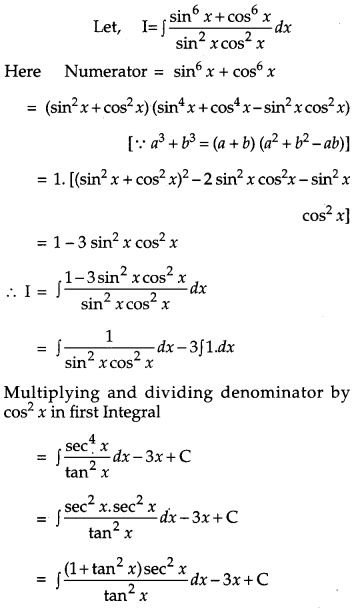
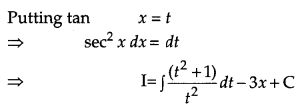
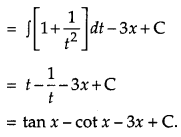
OR
Evaluate:
![]()
Solution:
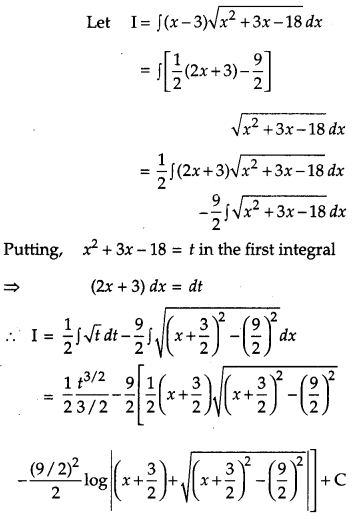
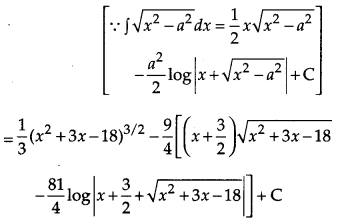
Question 18.
Find the particular solution of the differential equation \(e^{x} \sqrt{1-y^{2}} d x+\frac{y}{x} d y=0\), given that y = 1 when x = 0. [4]
Solution:
The given differential equation is
\(e^{x} \sqrt{1-y^{2}} d x+\frac{y}{x} d y=0\)

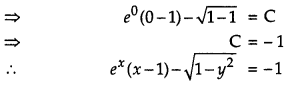
Question 19.
Solve the following differential equation: [4]
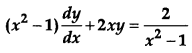
Solution:
The given differential equation is
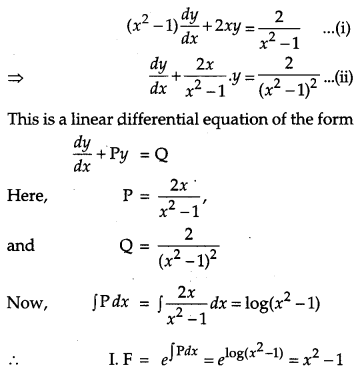
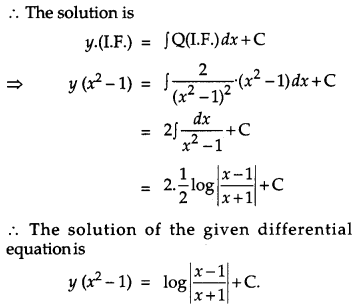
Question 20.
Prove that, for any three vectors : \(\vec{a}, \vec{b}, \vec{c}\)\(\overrightarrow{[a}+\vec{b}, \vec{b}+\vec{c}, \vec{c}+\vec{a}]=2[\vec{a}, \vec{b}, \vec{c}]\) [4]
Solution:
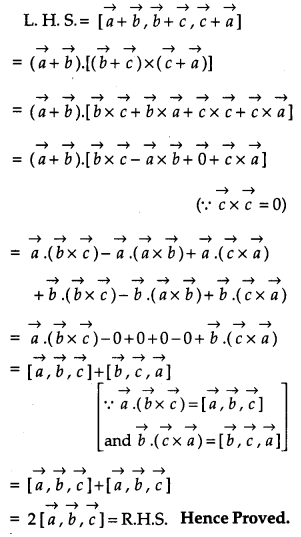
OR
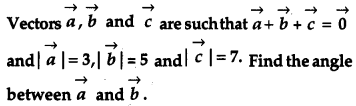
Solution:
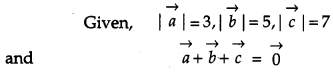
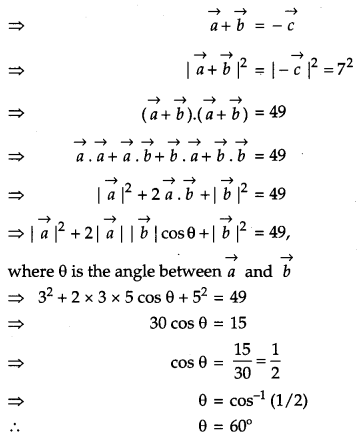
Question 21.
Show that the lines \(\frac{x+1}{3}=\frac{y+3}{5}=\frac{z+5}{7}\) and \(\frac{x-2}{1}=\frac{y-4}{3}=\frac{z-6}{5}\) intersect. Also find their point of intersection. [4]
Solution:
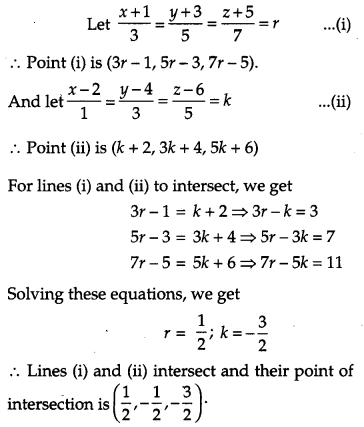
Question 22.
Assume that each bom child is equally likely to be a boy or a girl. If a family has two children, what is the conditional probability that both are girls ? Given that
(i) the youngest is a girl.
(ii) atleast one is a girl. [4]
Solution:
The sample space
S = {B1B2, B1G2, G1G2, G1B2}
⇒ n(S) – 4
Let A be the event that both children are girls, B be the event that the youngest child is a girl and C be the event that atleast one of the children is a girl. Then

![]()
Section – C
Question 23.
Two schools P and Q want to award their selected students on the values of Discipline, Politeness and Punctuality. The school P wants to award ₹ x each, ₹ y each and ₹ z each for the three respective values to its 3, 2 and 1 students with a total award money of ₹ 1,000. School Q wants to spend ₹ 1,500 to award its 4, 1 and 3 students on the respective values (by giving the same award money for the three values as before). If the total amount . of awards for one prize on each value is ₹ 600, using matrices, find the award money for each value.
Apart from the above three values, suggest one more value for awards. [6]
Solution:
The awards for Discipline, Politeness and Punctuality is ₹ x, ₹ y and ₹ z respectively. According to question,
3x + 2y + z = 1,000
4x + y + 3z = 1,500
x + y + z = 600
The given equation can be written in matrix form,
AX = B …(i)

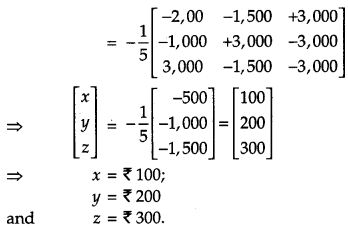
A part from the three values, Discipline, Politeness and Punctuality, another value for award, should be Hard Work.
Question 24.
Show that the semi-vertical angle of the cone of the maximum volume and of given slant height is \(\cos ^{-1} \frac{1}{\sqrt{3}}\). [6]
Solution:
Let θ be the semi-vertical angle of a cone, h its height, r base radius and slant height:

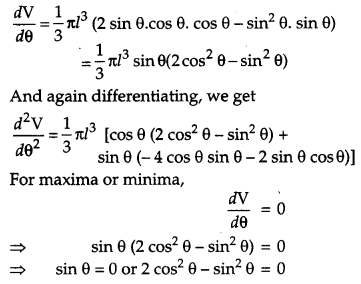
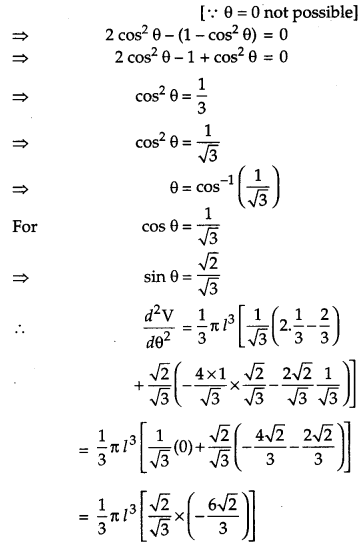
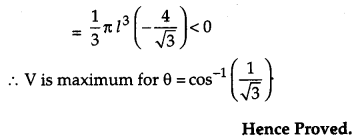
Question 25.
Evaluate: [6]
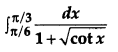
Solution:
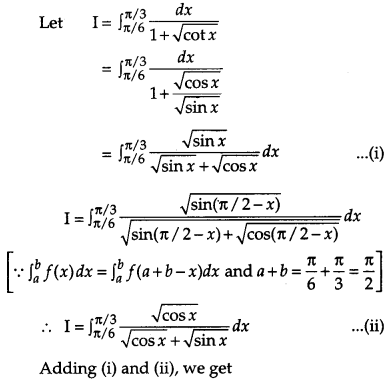
Question 26.
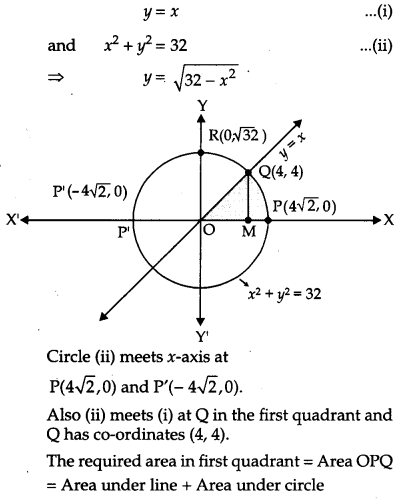
Find the area of the region in the first quadrant enclosed by the x-axis, the line y = x and circle x2 + y2 = 32. [6]
Solution:
Equation of the line and the circle are:
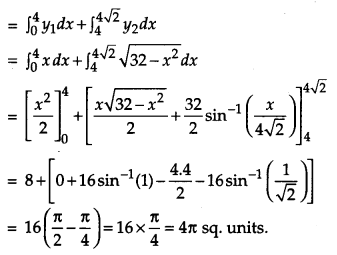
Question 27.
Find the distance between the point (7, 2, 4) and the plane determined by the points A (2, 5, – 3), B (- 2, – 3, 5) and C (5, 3, – 3). [6]
Solution:
The plane passing through A (2, 5, – 3) is
a(x – 2) + b(y – 5) + c(z + 3) = 0 …(i)
It passes through B (- 2, – 3, 5) and C (5, 3, – 3);
So -4a – 8b + 8c = 0 …(ii)
3a – 2b + 0c = 0 …(iii)
Solving equation (ii) and (iii), we get
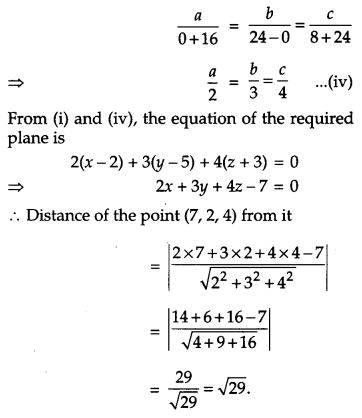
OR
Find the distance of the point (- 1, – 5, – 10) from the point of intersection of the line \(\vec{r}=2 \hat{i}-\hat{j}+2 \hat{k}+\lambda(3 \hat{i}+4 \hat{j}+2 \hat{k})\) and the plane \(\vec{r} \cdot(\hat{i}-\hat{j}+\hat{k})=5\).
Solution:
The given plane is

Question 28.
A dealer in rural area wishes to purchase a number of sewing machines. He has only ₹ 5,760 to invest and has space for at most 20 items for storage. An electronic sewing machine cost him ₹ 360 and a manually operated sewing machine ? 240. He can sell an electronic sewing machine at a profit of ₹ 22 and a manually operated sewing machine at a profit of ₹ 18. Assuming that he can sell all the items that he can buy, how should he invest his money in order to maximize his profit ? Make it as a LPP and solve it graphically. [6]
Solution:
Let the dealer buy x electronic and y manually operated sewing machines. The LPP is Maximize
Z = 22x + 18y
Subject to constraints:
x + y ≤ 20
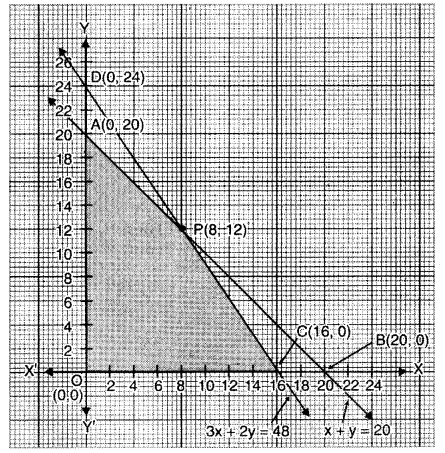
∴ The feasible region is OCPAO which is shaded in the figure.
The vertices of the feasible region are O (0, 0), C (16, 0), A (0, 20).
P is the point of intersection of the lines :
x + y = 20 and 3x + 2y = 48.
Solving these equations, we get point P (8, 12). The value of objective function Z = 22x + 18y at these vertices are as follows :
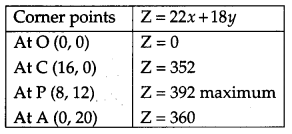

∴ The maximum profit is ₹ 392 when 8 electronic and 12 manually operated machines are purchased.
Question 29.
A card from a pack of 52 playing cards is lost. From the remaining cards of the pack three cards are drawn at random (without replacement) and are found to be all spades. Find the probability of the lost card being a spade. [6]
Solution:
Let E1, E2, E3, E4 and A be the events defined as below:
E1 = the missing card is a heart card
E2 = the missing card is a spade card
E3 = the missing card is a club card
E4 = the missing card is a diamond card
A = drawing three spades cards from the remaining cards.
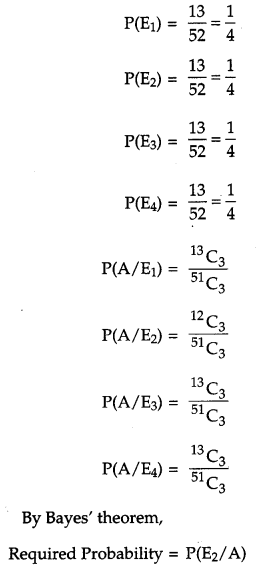

OR
From a lot of 15 bulbs which include 5 defectives, a sample of 4 bulbs is drawn one by one with replacement. Find the probability distribution of number of defective bulbs. Hence find the mean of the distribution.
Solution:
Let D be the event of drawing a defective bulb and X denote the variable showing the number of defective bulbs in 4 draws. Then
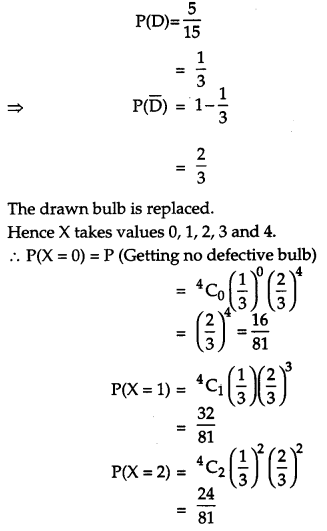

CBSE Previous Year Question Papers Class 12 Maths 2014 Delhi Set II
Note: Except for the following questions, all the remaining questions have been asked in previous set.
Section – A
Question 9.
Evaluate: \(\int \cos ^{-1}(\sin x) d x\). [1]
Solution:
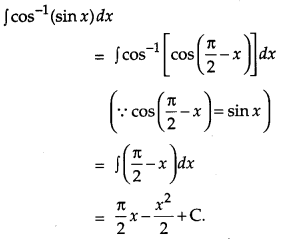
Question 10.
If vectors \(\vec{a} \text { and } \vec{b}\) are such that, \(|\vec{a}|=3\), \(|\vec{b}|=\frac{2}{3} \text { and } \vec{a} \times \vec{b}\) is a unit vector, then write the angle between \(\vec{a} \text { and } \vec{b}\). [1]
Solution:
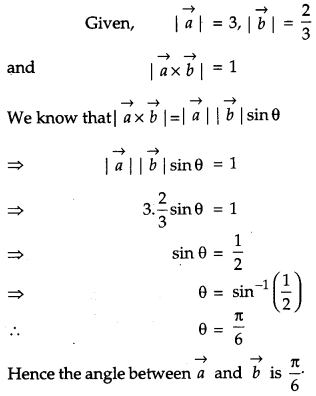
Section – B
Question 19.
Prove the following using properties of determinants: [4]
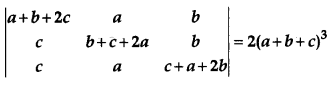
Solution:

Question 20.
Differentiate \(\tan ^{-1}\left(\frac{x}{\sqrt{1-x^{2}}}\right)\) with respect to \(\sin ^{-1}(2 x \sqrt{1-x^{2}})\). [4]
Solution:
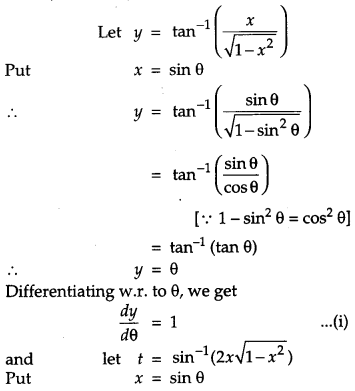
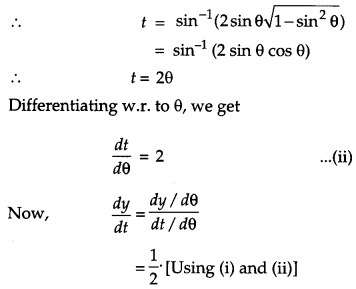
Question 21.
Solve the following differential equation : [4]
![]()
Solution:
The given differential equation is
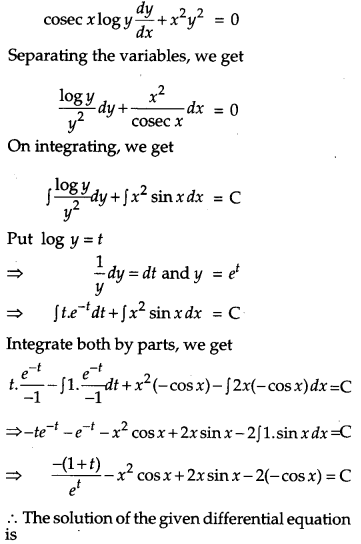
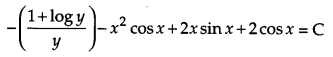
Question 22.
Show that the lines \(\frac{5-x}{-4}=\frac{y-7}{4}=\frac{z+3}{-5}\) and \(\frac{x-8}{7}=\frac{2 y-8}{2}=\frac{z-5}{3}\) are coplanar. [4]
Solution:
The given lines are
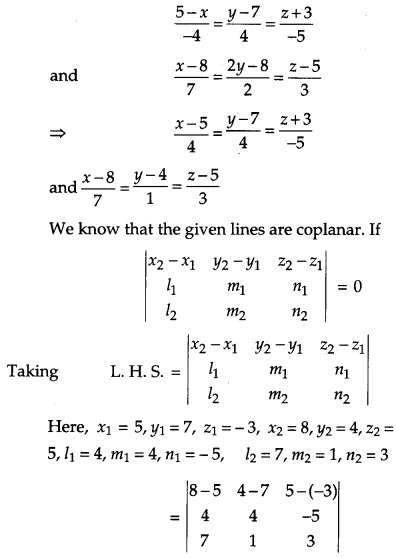
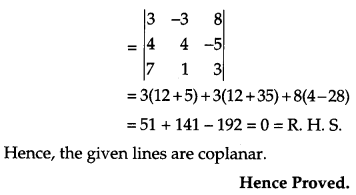
Section – C
Question 28.
Evaluate: [6]
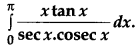
Solution:
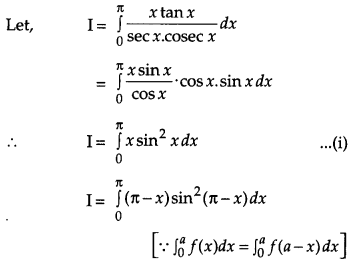
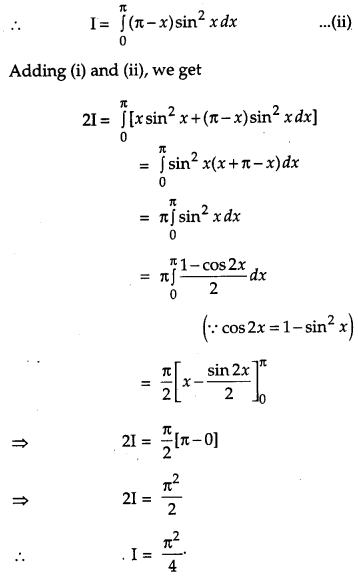
Question 29.
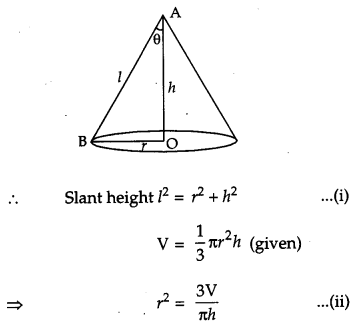
Prove that the semi-vertical angle of the right circular cone of given volume and least curved surface area is \(\cot ^{-1} \sqrt{2}\). [6]
Solution:
Let r, h, l, V and S be the base radius, height, slant height, volume (given) and curved surface of the cone respectively. Then
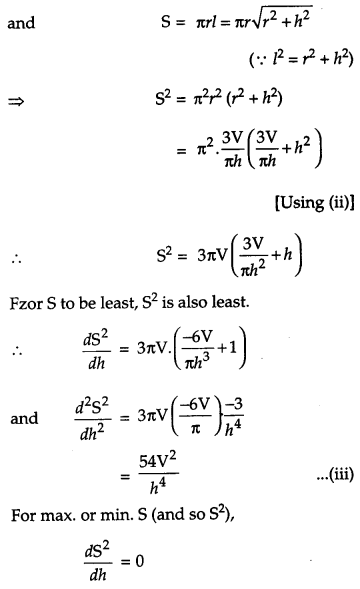

CBSE Previous Year Question Papers Class 12 Maths 2014 Delhi Set III
Note: Except for the following questions, all the remaining questions have been asked in previous sets.
Section – A
Question 9.
Evaluate: [1]
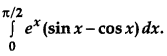
Solution:
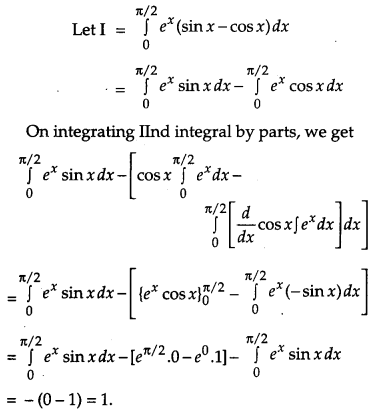
Question 10.
Write a unit vector in the direction of the sum of the vectors \(\vec{a}=2 \hat{i}+2 \hat{j}-5 \hat{k} \text { and } \vec{b}=2 \hat{i}+\hat{j}-7 \hat{k}\). [1]
Solution:

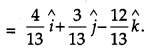
Section – B
Question 19.
Using properties of determinants, prove the following: [4]
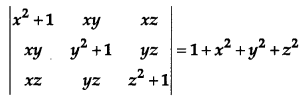
Solution:
Taking L. H. S
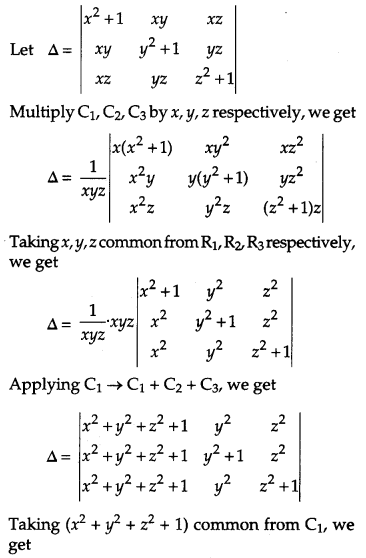
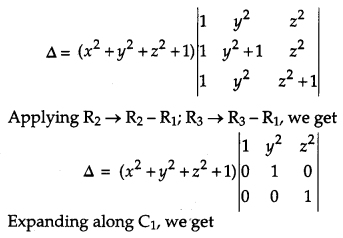
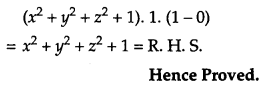
Question 20.
Differentiate \(\tan ^{-1}\left(\frac{\sqrt{1+x^{2}}-1}{x}\right)\) with respect to \(\sin ^{-1}\left(\frac{2 x}{1+x^{2}}\right)\), when x ≠ 0. [4]
Solution:


Question 21.
Find the particular solution of the differential equation \(\frac{d y}{d x}=\frac{x(2 \log x+1)}{\sin y+y \cos y}\) given that y = \(\frac{\pi}{2}\) when x = 1. [4]
Solution:
The given differential equation is
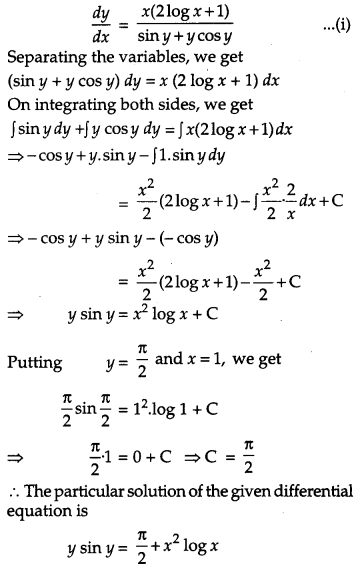
Question 22.
Show that lines \(\vec{r}=(\hat{i}+\hat{j}-\hat{k})+\lambda(3 \hat{i}-\hat{j})\) and \(\vec{r}=(4 \hat{i}-\hat{k})+\mu(2 \hat{i}+3 \hat{k})\) interesect. Also find their point of intersection. [4]
Solution:
The equation of given lines are
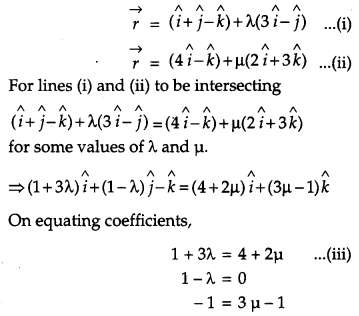

Section – C
Question 28.
Evaluate: [6]
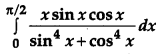
Solution:
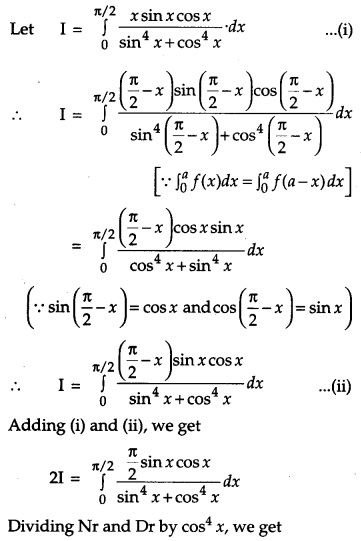
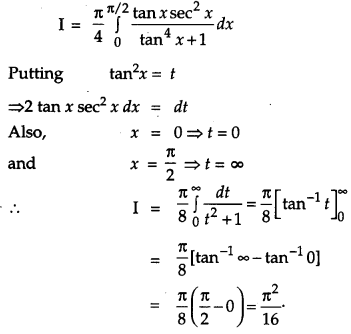
Question 29.
Of all the closed right circular cylindrical cans of volume 128 π cm3, find the dimensions of the can which has minimum surface area. [6]
Solution:
Let r cm be the base radius and h cm be the height of the closed cylindrical cans of given volume = 128 π cm3.