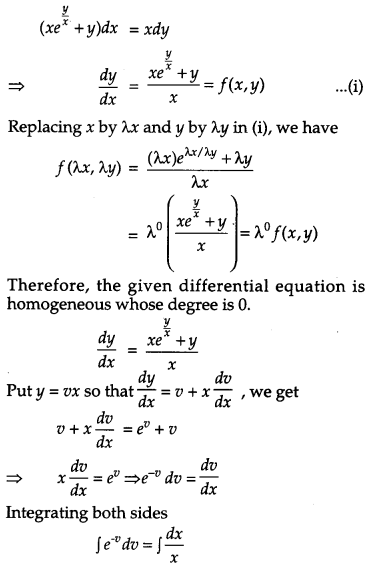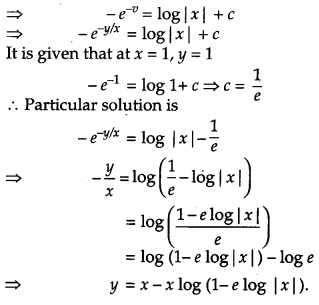CBSE Previous Year Question Papers Class 12 Maths 2013 Delhi
Time allowed: 3 hours
Maximum marks : 100
General Instructions:
- All questions are compulsory.
- The question paper consists of 29 questions divided into four sections A, B, C and D. Section A comprises of 4 questions of one mark each, Section B comprises of 8 questions of two marks each, Section C comprises of 11 questions of four marks each and Section D comprises of 6 questions of six marks each.
- All questions in Section A are to be answered in one word, one sentence or as per the exact requirement of the question.
- There is no overall choice. However, internal choice has been provided in 1 question of Section A, 3 questions of Section B, 3 questions of Section C and 3 questions of Section D. You have to attempt only one of the alternatives in all such questions.
- Use of calculators is not permitted. You may ask for logarithmic tables, if required.
CBSE Previous Year Question Papers Class 12 Maths 2013 Delhi Set I
Section – A
Question 1.
Write the principal value of tan-1(1) + cos-1\(\left(-\frac{1}{2}\right)\). [1]
Solution:
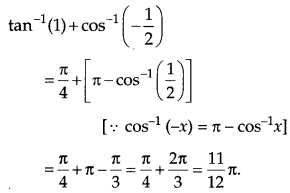
Question 2.
Write the value of tan 2 tan(2 tan-1\(\frac{1}{5}\)). [1]
Solution:
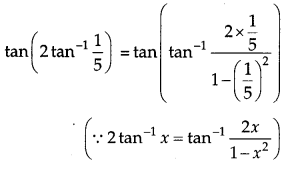
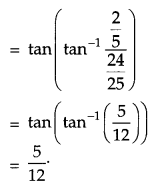
Question 3.
Find the value of a if
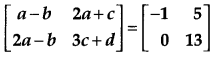 [1]
[1]
Solution:
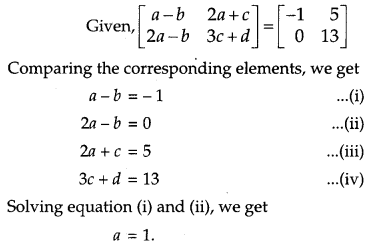
Question 4.
If \(\left|\begin{array}{ll}{x+1} & {x-1} \\ {x-3} & {x+2}\end{array}\right|=\left|\begin{array}{rr}{4} & {-1} \\ {1} & {3}\end{array}\right|\) then write the value of x.
Solution:
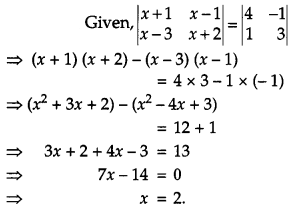
Question 5.
If \(\left[\begin{array}{rrr}{9} & {-1} & {4} \\ {-2} & {1} & {3}\end{array}\right]=\mathbf{A}+\left[\begin{array}{rrr}{1} & {2} & {-1} \\ {0} & {4} & {9}\end{array}\right]\), then find the matrix A. [1]
Solution:
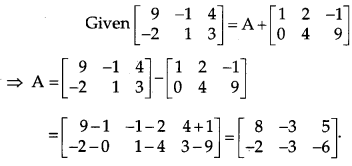
Question 6.
Write the degree of the differential equation [1]
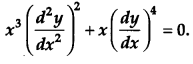
Solution:
The degree of the given differential equation is 2.
Question 7.
If \(\vec{a}=x \hat{i}+2 \hat{j}-z \hat{k} \text { and } \vec{b}=3 \hat{i}-y \hat{j}+\hat{k}\) are two equal vectors, then write the value of x + y + z. [1]
Solution:
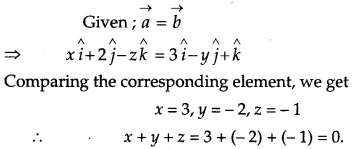
Question 8.
If a unit vector \(\vec{a}\) makes angle \(\frac{\pi}{3}\) with \(\hat{i}, \frac{\pi}{4}\) with \(\hat{j}\) and an acute angle θ with k then find the value of θ. [1]
Solution:
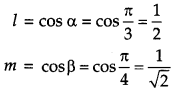
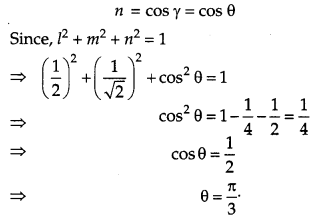
Question 9.
Find the cartesian equation of the line which passes through the point (- 2, 4, – 5) and is parallel to the line [1]
![]()
Solution:
Direction ratios of the line parallel to
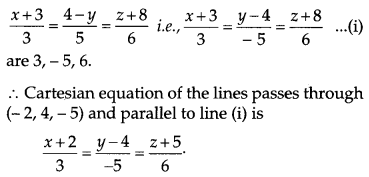
Question 10.
The amount of pollution content added in air in a city to x-diesel vehicles is given by P(x) = 0.005x3 + 0.02x2 + 30x. Find the marginal increase in pollution content when 3 diesel vehicles are added and write which value is indicated in the above question. [1]
Solution:
Here, pollution content is given by
P(x) = 0.005x3 + 0.02x2 + 30x
where x is the number of diesel vehicles.

The value indicated in the question is diesel vehicles causes environmental pollution.
Section – B
Question 11.
Show that the function f in A = R-\(\left\{\frac{2}{3}\right\}\) defined as f(x) = \(\frac{4 x+3}{6 x-4}\) is one-one and onto. Hence find f-1. [4]
Solution:
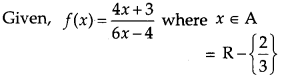

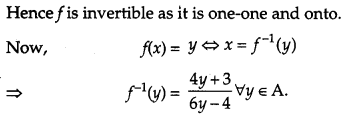
Question 12.
Find the value of the following:
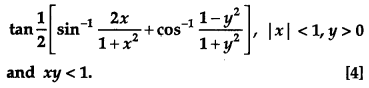
Solution:
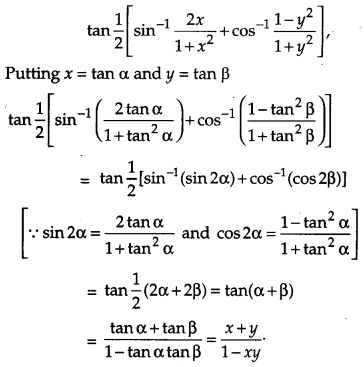
OR
Prove that:
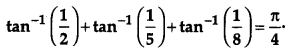
Solution:
L. H. S
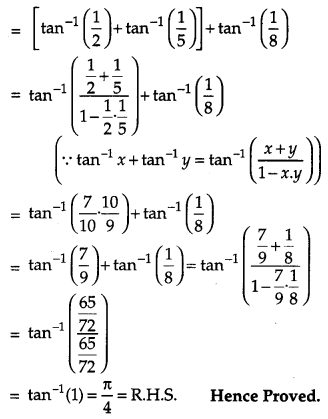
Question 13.
Using properties of determinants, prove the following: [4]
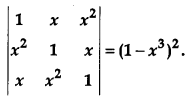
Solution:
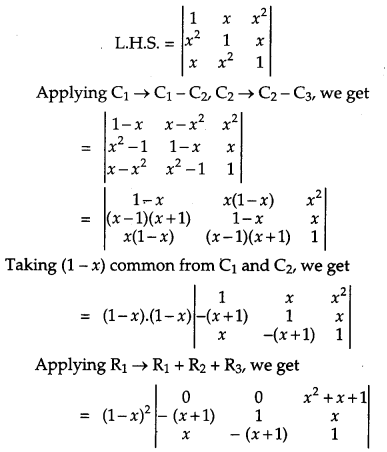
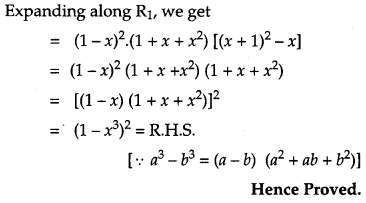
Question 14.
Differentiate the following function with respect to x:
(log x)x + xlogx [4]
Solution:
Let, y = (log x)x + xlogx

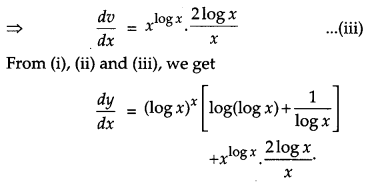
Question 15.
If y = log[x + \(\sqrt{x^{2}+a^{2}}\)], show that [4]
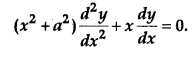
Solution:

Question 16.
Show that the function f(x) = | x – 3|, x ϵ R, is continuous but not differentiable at x = 3. [4]
Solution:
Given, f(x) = | x – 3|, x ϵ R

OR
If x = a sin t and y = a (cos t + log tan t/2), find \(\frac{d^{2} y}{d x^{2}}\).
Solution:
Given, x = a sin t


Question 17.
Evaluate: [4]
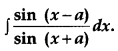
Solution:
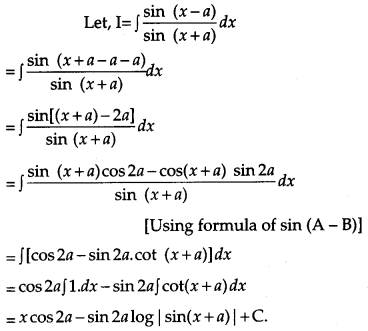
OR
Evaluate:
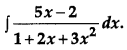
Solution:

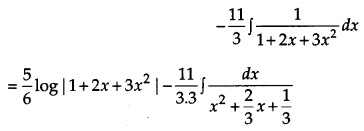
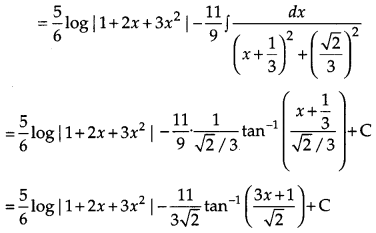
Question 18.
Evaluate: [4]
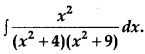
Solution:

Question 19.
Evaluate: [4]
![]()
Solution:
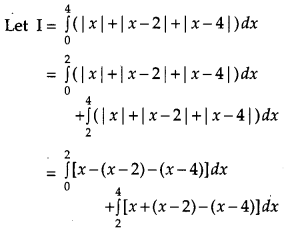
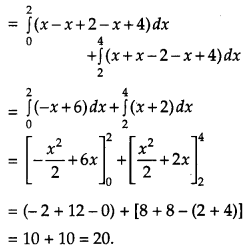
Question 20.
If \(\vec{a} \text { and } \vec{b}\) are two vectors such that \(|\vec{a}+\vec{b}|=|\vec{a}|\), then prove that vector \(2 \vec{a}+\vec{b}\) is perpendicular to vector \(\vec{b}\). [4]
Solution:
Given,

Question 21.
Find the coordinates of the point, where the line \(\frac{x-2}{3}=\frac{y+1}{4}=\frac{z-2}{2}\) intersects the plane x – y + z – 5 = 0. Also find the angle between the line and the plane. [4]
Solution:
Equation of the line is
\(\frac{x-2}{3}=\frac{y+1}{4}=\frac{z-2}{2}\) = k (say) ..(i)
∴ Point on line is (3k + 2, 4k – 1, 2k + 2).
If it lies on the plane x – y + z – 5 = 0 …(ii)
then (3k + 2) – (4k – 1) + (2k + 2) – 5 = 0
⇒ 3k + 2- 4k + 1 + 2k – 3 = 0
⇒ k = 0
∴ Point is (2, – 1, 2)
(2, – 1, 2) is the point on line (i), where it intersects (ii).
If 0 is the angle between line (i) and plane (ii), then
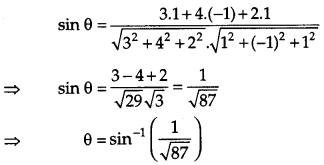
OR
Find the vector equation of the plane which contains the line of intersection of the planes \(\vec{r} \cdot(\hat{i}+2 \hat{j}+3 \hat{k})-4=0 \quad \text { and } \vec{r} \cdot(2 \hat{i}+\hat{j}-\hat{k})+5=0\) and which is perpendicular to the plane
\(\vec{r} \cdot(5 \hat{i}+3 \hat{j}-6 \hat{k})+8=0\)
Solution:
Given planes are

Question 22.
A speaks truth in 60% of the cases, while B in 90% of the cases. In what percent of cases are they likely to contradict each other in stating the same fact ? In the cases of contradiction do you . think, the statement of B will carry more weight as he speaks truth in more number of cases then A? [4]
Solution:
Probability of A speaking the truth is
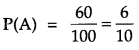

Section – C
Question 23.
A school wants to award its students for the values of Honesty, Regularity and Hard work with a total cash award of ₹ 6,000. Three times the award money for Hard work added to that given for honesty amounts to ₹ 11,000. The award money given for Honesty and Hard work together is double the one given for Regularity. Represent the above situation algebraically and find the award money for each value, using matrix method. Apart from these values namely, Honesty, Regularity and Hard work, suggest one more value which the school must include for awards. [6]
Solution:
Let award for honesty be ₹ x
award for regularity be ₹ y
and award for hardwork be ₹ z.
According to question,
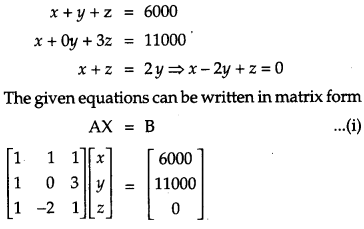
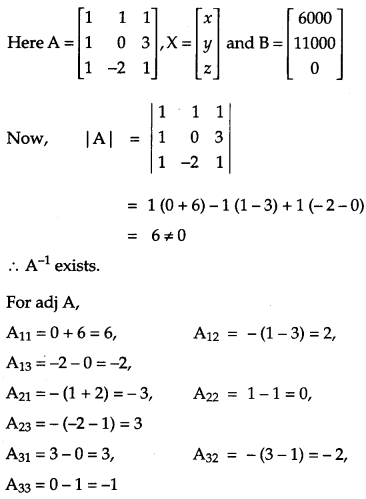

Apart from honesty, regularity and hard work, the school must include an award for a student to be well behaved.
Question 24.
Show that the height of the cylinder of maximum volume, that can be inscribed in a sphere of radius R is \(\frac{2 \mathbf{R}}{\sqrt{3}}\). Also find the maximum volume. [6]
Solution:
From the figure:
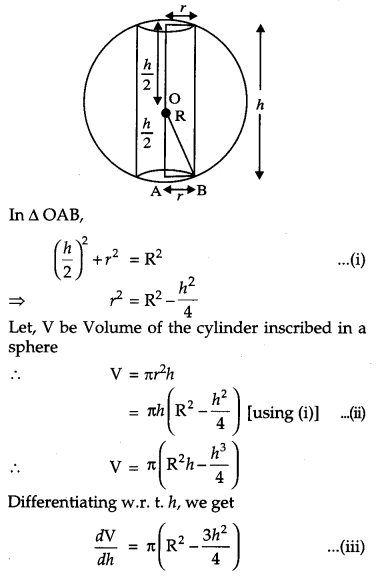

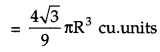
OR
Find the equation of the normal at a point on the curve x2 = 4y which passes through the point (1, 2). Also find the equation of the corresponding tangent.
Solution:
The given curve is
x2 = 4y …(i)
Let (x1, y1) be the required point on curve
x12 = 4y1 …(ii)
Differentiating eq. (i) w.r.t. x, we get
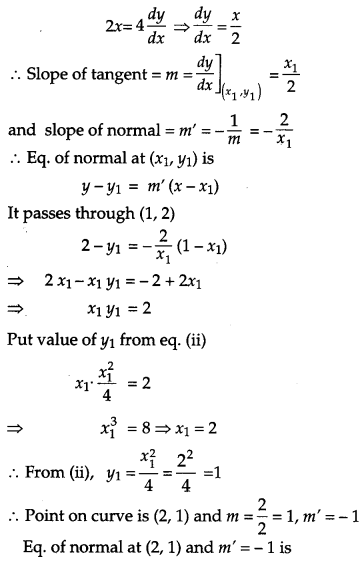
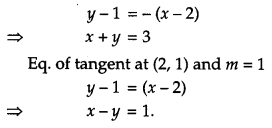
Question 25.
Using integration, find the area bounded by the curve x2 = 4y and the line x = 4y – 2. [6]
Solution:
The equation of the given curves are :
x2 = 4y …(i)
x = 4y – 2 …(ii)
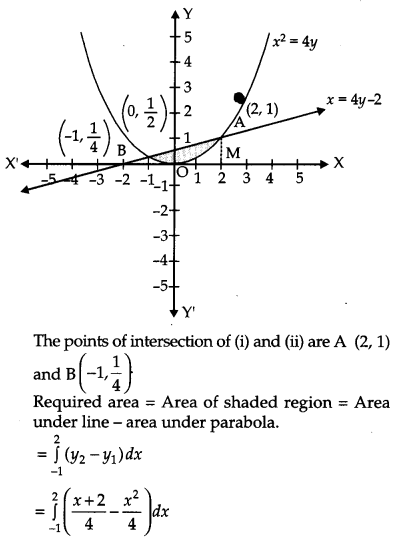
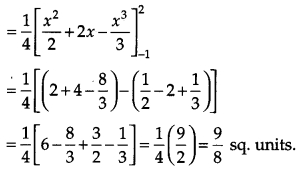
OR
Using integration, find the area of the region enclosed between the two circles x2 + y2 = 4 and (x- 2 )2 + y2 = 4.
Solution:
The given circles are :
x2 + y2 = 4 ..(i)
and (x – 2)2 + y2 = 4 …(ii)
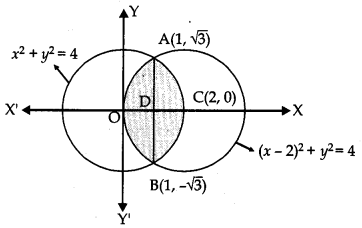

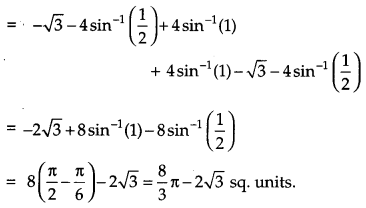
Question 26.
Show that the differential equation 2yex/ydx + (y – 2 xex/y) dy = 0 is homogeneous. Find the particular solution of this differential equation, given that x = 0, when y = 1. [6]
Solution:
The given differential equation is
2yex/y dx + (y – 2xex/y) dy = 0
Separate the given differential equation, we get
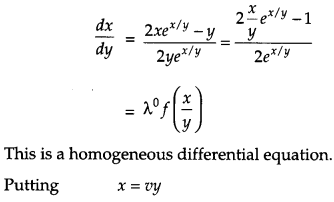
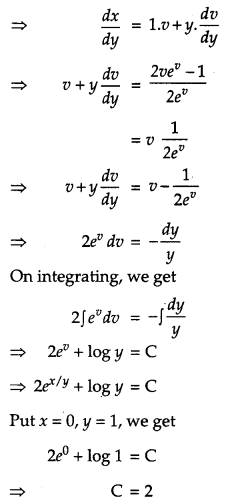
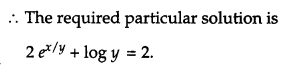
Question 27.
Find the vector equation of the plane passing through three points with position vectors \(\hat{i}+\hat{j}-2 \hat{k}, 2 \hat{i}-\hat{j}+\hat{k} \text { and } \hat{i}+2 \hat{j}+\hat{k}\) Also find the coordinates of the point of intersection of this plane and the line \(\vec{r}=3 \hat{i}-\hat{j}-\hat{k}+\lambda(2 \hat{i}-2 \hat{j}+\hat{k})\). [6]
Solution:
The given points are
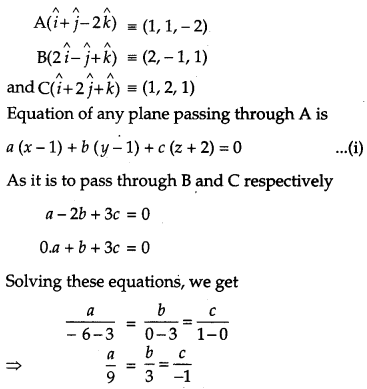

Question 28.
A cooperative society of farmers has 50 hectares of land to grow two crops A and B. The profits from crops A and B per hectare are estimated as ₹ 10,500 and ₹ 9,000 respectively. To control weeds, a liquid herbicide has to be used for crops A and B at the rate of 20 litre and 10 litre per hectare, respectively. Further not more than 800 litres of herbicide should be used in order to protect fish and wildlife using a pond which collects drainage from this land. Keeping in mind that the protection of fish and other wildlife is more important than earning profit, how much land should be allocated to each crop so as to maximize the total profit ? Form an LPP from the above and solve it graphically. Do you agree with the message that the protection of wildlife is utmost necessary to preserve the balance in environment ? [6]
Solution:
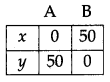
Let x hectare and y hectare be allotted to grow crops A and B respectively. Then the L.P.P. is maximize:
Z = 10,500 x + 9,000 y subject to constraints,
x + y ≤ 50
20x + 10y ≤ 800
=> 2x + y ≤ 80
and x ≥ 0, y ≥ 0
First we draw the line AB and CD whose equations are
x + y = 50 …(i)
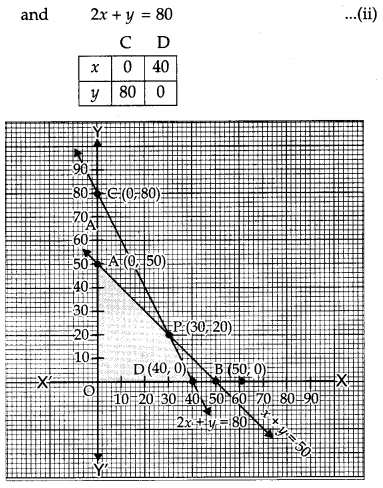
∴ The feasible region is ODPAO which is shaded in the figure.
P is the point of intersection of the lines
x + y = 50
2x + y =80
Solving these equations, we get point P (30, 20).
The vertices of the feasible region are (0, 0), D (40, 0), P (30, 20) and A (0, 50).The value of objective function Z = 10,500 x + 9,000 y at these vertices are as follows :
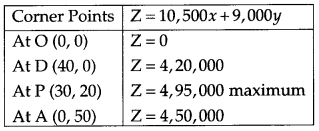
∴ The maximum profit is 4,95,000 at point P (30, 20). Yes, I agree with the message in the question.
Question 29.
Assume that the chances of a patient having a heart attack is 40%. Assuming that a meditation and yoga course reduces the risk of heart attack by 30% and prescription of certain drug reduces its chance by 25%. At a time a patient can choose any one of the two options with equal possibilities. It is given that after going through one of the two options, the patient selected at random suffers a heart attack. Find the probability that the patient followed a course of meditation and yoga. Interpret the result and state which of the above stated methods is more beneficial for the patient. [6]
Solution:
Let E1 be taking a course of meditation and yoga and E2 be taking a course of drugs.
A be the patient gets a heart attack.
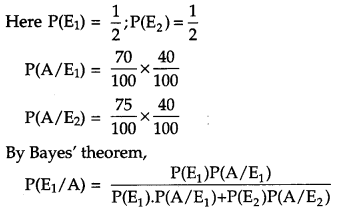
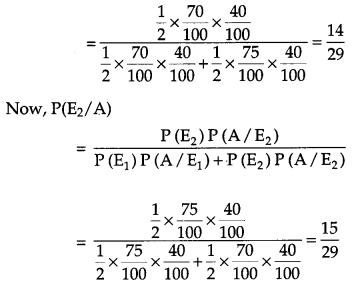
Since, P(E1/A) < P(E2/A) the course of yoga and meditation is more beneficial for a person having chances of heart attack.
CBSE Previous Year Question Papers Class 12 Maths 2013 Delhi Set II
Note : Except for the following questions, all the remaining questions have been asked in previous set.
Section – A
Question 3.
Find the value of b if [1]
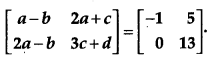
Solution:
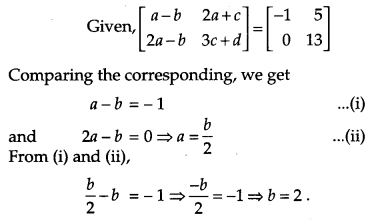
Question 9.
Write the degree of the differential equation [1]
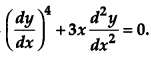
Solution:
The degree of the differential equation
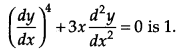
Section – B
Question 16.
P speaks truth in 70% of the cases and Q in 80% of the cases. In what percent of cases are they likely to agree in stating the same fact ?
Do you think, when they agree, means both are speaking truth ? [4]
Solution:
Probability of P speaking the truth is

No, not necessarily when they agree there may be case in which they both does not speak truth.
Question 18.
If \(\vec{a}=\hat{i}+\hat{j}+\hat{k} \text { and } \vec{b}=\hat{j}-\hat{k}\), find a vector \(\vec{c}\), such that \(\vec{a} \times \vec{c}=\vec{b} \text { and } \vec{a} \cdot \vec{c}=3\). [4]
Solution:
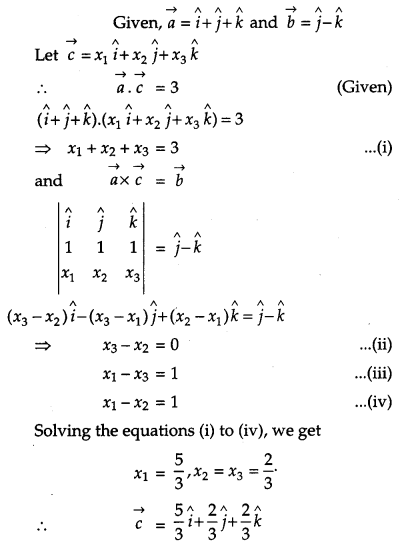
![]()
Question 19.
Evaluate: \(\int_{1}^{3}[|x-1|+|x-2|+|x-3|] d x\). [4]
Solution:
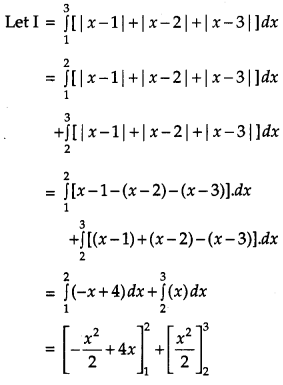
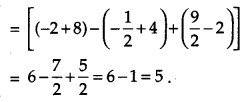
Question 20.
Evaluate : [4]
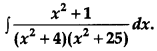
Solution:
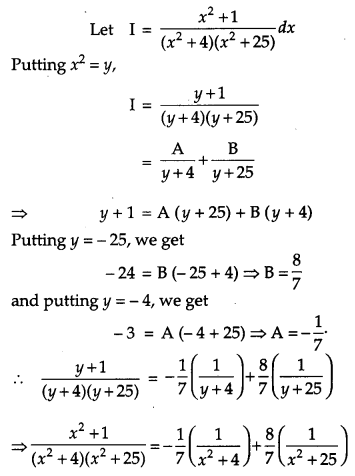
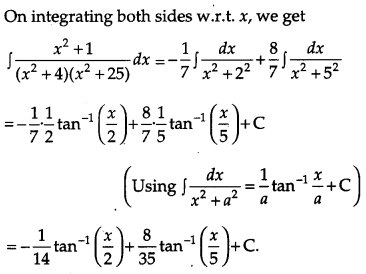
Section – C
Question 28.
Show that the differential equation \(x \frac{d y}{d x} \sin \left(\frac{y}{x}\right)+x-y \sin \left(\frac{y}{x}\right)=0\) is homogeneous. Find the particular solution of this differential equation given that x = 1 when y = \(\frac{\pi}{2}\). [6]
Solution:
The given differential equation is
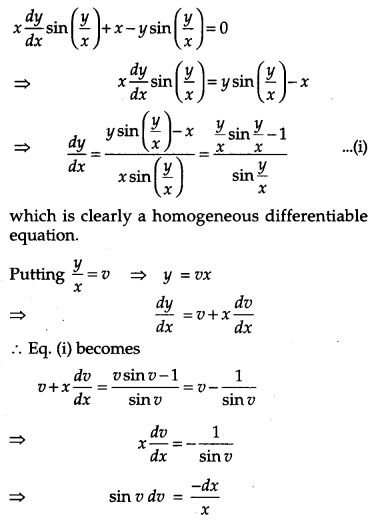
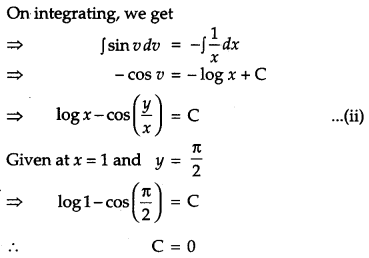
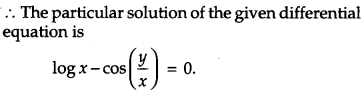
CBSE Previous Year Question Papers Class 12 Maths 2013 Delhi Set III
Note : Except for the following questions, all the remaining questions have been asked in previous sets.
Section – A
Question 2.
Write, unit vector in the direction of the sum of vectors \(\vec{a}=2 \hat{i}-\hat{j}+2 \hat{k} \text { and } \vec{b}=-\hat{i}+\hat{j}+3 \hat{k}\). [1]
Solution:
\(\vec{a}=2 \hat{i}-\hat{j}+2 \hat{k} \text { and } \vec{b}=-\hat{i}+\hat{j}+3 \hat{k}\)
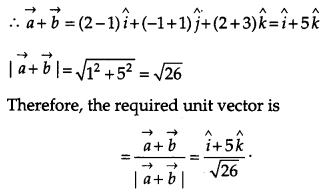
Question 4.
Write the degree of the differential equation [1]
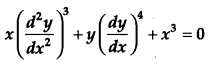
Solution:
The given differential equation is
Section – B
Question 11.
A speaks truth in 75% of the cases, while B in 90% of the cases. In what percent of cases are they likely to contradict each other in stating the same fact ? Do you think that statement of B is true ? [4]
Solution:
Let, the probability that A and B speak truth be P(A) and P(B) respectively.

Question 13.
Using vectors, find the area of the triangle ABC with vertices A (1, 2, 3), B (2, – 1, 4) and C (4, 5, -1). [4]
Solution:
The vertices of ∆ ABC are A (1, 2, 3), B (2, -1, 4) and C (4, 5, – 1).
∴ \(\overrightarrow{\mathrm{AB}}\) = Position vector of B – Position vector of A
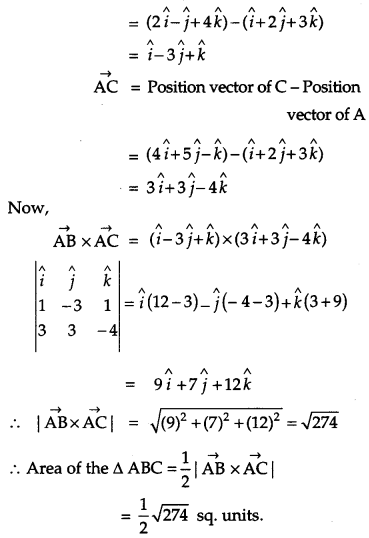
Question 14.
Evaluate: \(\int_{2}^{5}[|x-2|+|x-3|+|x-5|] d x\). [1]
Solution:
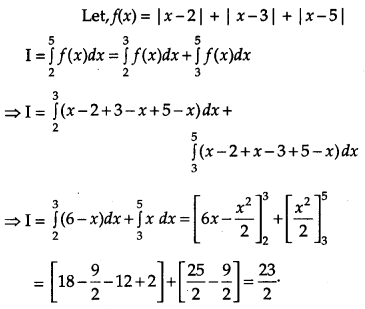
Question 15.
Evaluate: [4]
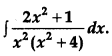
Solution:
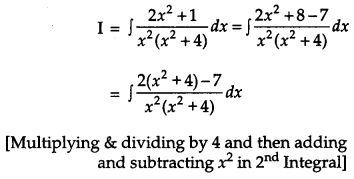
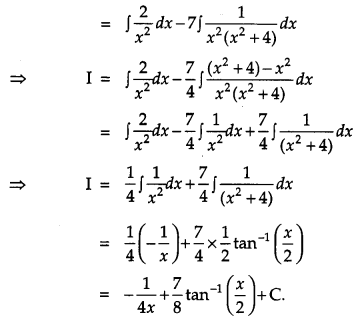
Section – C
Question 25.
Find the coordinates of the point where the line through (3, -4, -5) and (2, – 3, 1) crosses the plane, passing through the points (2, 2, 1), (3, 0, 1) and (4, -1, 0). [6]
Solution:
The equation of the straight line passing through the point (3, -4, -5) and (2, – 3, 1) is
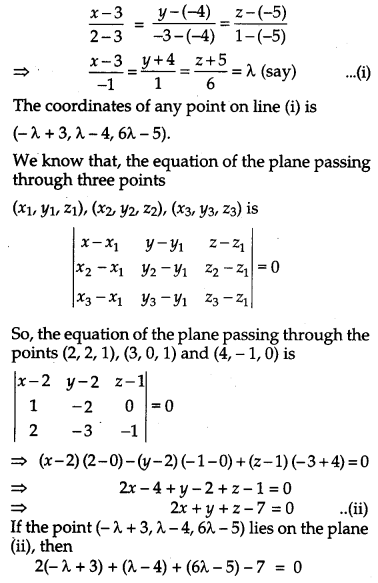
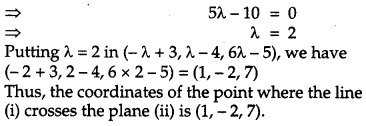
Question 26.
Show that the differential equation (xey/x + y) dx = xdy is homogeneous. Find the particular solution of this differential equation, given that x = 1 when y = 1. [6]
Solution:
The given differential equation is