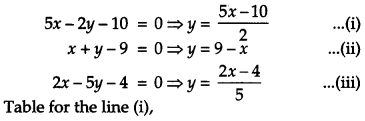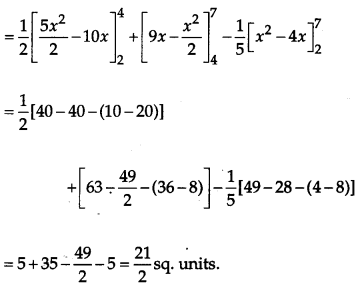CBSE Previous Year Question Papers Class 12 Maths 2012 Delhi
Time allowed: 3 hours
Maximum marks : 100
General Instructions:
- All questions are compulsory.
- The question paper consists of 29 questions divided into four sections A, B, C and D. Section A comprises of 4 questions of one mark each, Section B comprises of 8 questions of two marks each, Section C comprises of 11 questions of four marks each and Section D comprises of 6 questions of six marks each.
- All questions in Section A are to be answered in one word, one sentence or as per the exact requirement of the question.
- There is no overall choice. However, internal choice has been provided in 1 question of Section A, 3 questions of Section B, 3 questions of Section C and 3 questions of Section D. You have to attempt only one of the alternatives in all such questions.
- Use of calculators is not permitted. You may ask for logarithmic tables, if required.
**Answer is not given due to the change in present syllabus
CBSE Previous Year Question Papers Class 12 Maths 2012 Delhi Set I
Section -A
Question 1.
If a line has direction ratios 2, -1, – 2, then what are its direction cosines ? [1]
Solution:
Given direction ratios are 2, -1, – 2
i.e., a = 2, b = -1, c = – 2.
Direction cosines are:
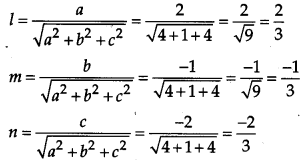
![]()
Question 2.
Find ‘λ’ when the projection of \(\vec{a}=\lambda \hat{i}+\hat{j}+4 \hat{k}\) on \(\vec{b}=2 \hat{i}+6 \hat{j}+3 \hat{k}\) is 4 units. [1]
Solution:
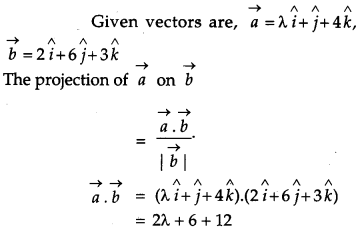
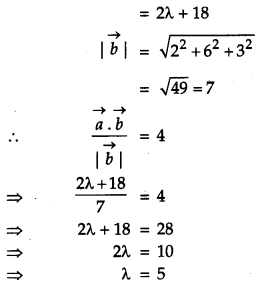
Question 3.
Find the sum of the vectors \(\vec{a}=\hat{i}-2 \hat{j}+\hat{k}\), \(\vec{b}=-2 \hat{i}+4 \hat{j}+5 \hat{k} \text { and } \vec{c}=\hat{i}-6 \hat{j}-7 \hat{k}\). [1]
Solution:
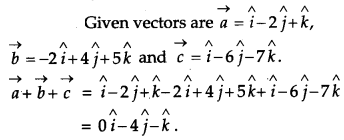
Question 4.
Evaluate: [1]
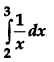
Solution:
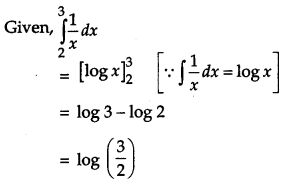
Question 5.
Evaluate: [1]
![]()
Solution:
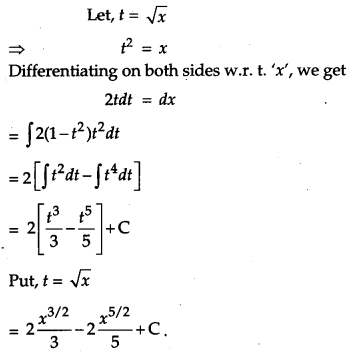
Question 6.
If ∆ = \(\left|\begin{array}{lll}{5} & {3} & {8} \\ {2} & {0} & {1} \\ {1} & {2} & {3}\end{array}\right|\), write the minor of the element a23. [1]
Solution:

Question 7.
If \(\left(\begin{array}{cc}{2} & {3} \\ {5} & {7}\end{array}\right)\left(\begin{array}{rr}{1} & {-3} \\ {-2} & {4}\end{array}\right)=\left(\begin{array}{cc}{-4} & {6} \\ {-9} & {x}\end{array}\right)\), write the value of x. [1]
Solution:
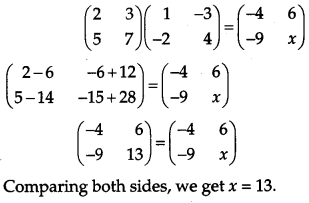
Question 8.
Simplify:
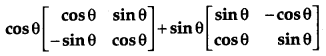 [1]
[1]
Solution:
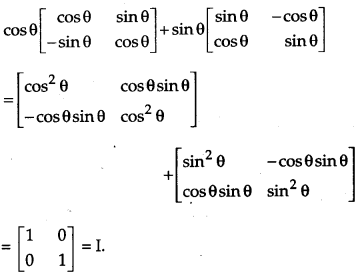
Question 9.
Write the principal value of
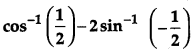 [1]
[1]
Solution:
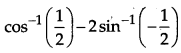
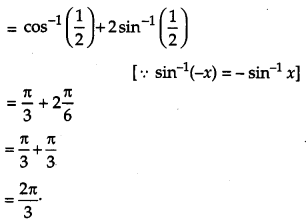
Question 10.
Let * be a ‘binary’ operation of N given by a * b = LCM (a, b) for all a, b ϵ N. Find 5 * 7.** [1]
Section – B
Question 11.
If (cos x)y = (cos y)x, find \(\frac{d y}{d x}\). [4]
Solution:
Given, (cos x)y = (cos y)x
Taking log on both sides, we get
log (cos x)y = log (cos y)x
⇒ y log cos x = x log cos y
On differentiating w.r.t. x, we get
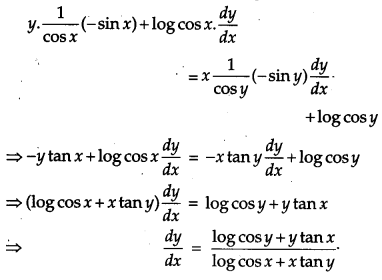
OR
If sin y = x sin(a + y), prove that \(\frac{d y}{d x}=\frac{\sin ^{2}(a+y)}{\sin a}\).
Solution:
Given, sin y = x sin(a + y)
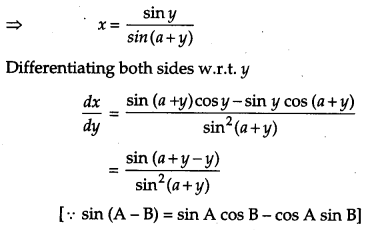
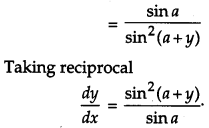
Question 12.
How many times must a man toss a fair coin, so that the probability of having at least one head is more than 80%? [4]
Solution:
Let us consider,
x = Number of times a man should toss a coin.
P(H) = Probability of getting atleast one head.
If x = 1, sample space will be H, T

Hence, a coin should be tossed 3 times in order to have the probability of getting atleast one head is more than 80%.
Question 13.
Find the vector and cartesian equations of the line passing through the point (1, 2, – 4) and perpendicular to the two lines \(\frac{x-8}{3}=\frac{y+19}{-16}\)\(=\frac{z-10}{7} \text { and } \frac{x-15}{3}=\frac{y-29}{8}=\frac{z-5}{-5}\). [4]
Solution:
Let, the direction ratios of required line be p, q, r and given that, line is perpendicular to two given lines,
Therefore, we get
3p – 16q + 7r = 0
3p + 8q – 5r = 0
On solving, we get
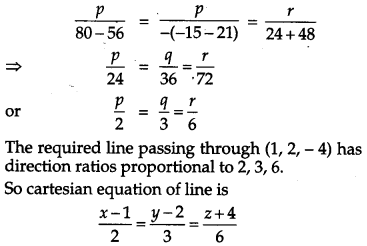
Equation of line passing through (1, 2, – 4) has direction ratios, proportional to 2, 3, 6.
i.e. in vector form, this line passes through point having position vector,

Question 14.
If \(\vec{a}, \vec{b}, \vec{c}\) are three vectors such that \(|\vec{a}|=5,|\vec{b}|\) = 12 and \(|\vec{c}|=13 \text { and } \vec{a}+\vec{b}+\vec{c}=\overrightarrow{0}\) find the value of \(\vec{a} \cdot \vec{b}+\vec{b} \cdot \vec{c}+\vec{c} \cdot \vec{a}\). [4]
Solution:
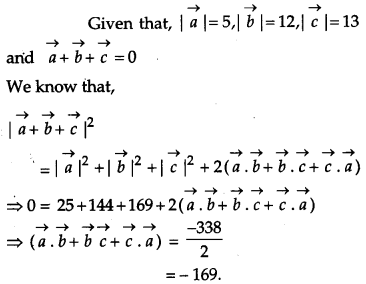
Question 15.
Solve the following differential equation :
![]() [4]
[4]
Solution:
The given differential equation is

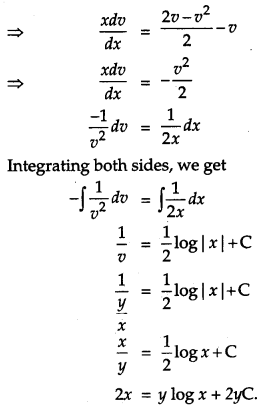
Question 16.
Find the particular solution of the following differential equation; \(\frac{d y}{d x}\) = 1 + x2 + y2 + x2y2, given that y = 1 when x = 0. [4]
Solution:

Question 17.
Evaluate:
![]() [4]
[4]
Solution:
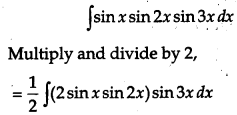
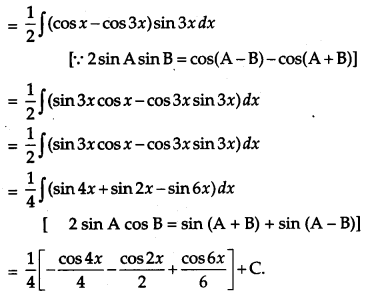
OR
Evaluate:
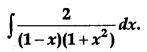
Solution:
By method of partial fractions:

Question 18.
Find the point on the curve y = x3 – l1x + 5 at which the equation of tangent is y = x – 11. [4]
Solution:
Given curve is y = x3 – 11x + 5 …..(i)
Slope of tangent to curve
![]()
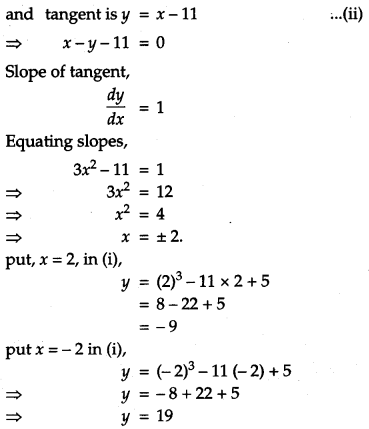
The points on the curve are, (2, – 9), (- 2, 19) Now, put these values in (ii)
-9 = 2 – 11
So, (2, – 9) is satisfying the tangent equation.
But (-2, 19) does not satisfy tangent equation.
Hence (2, – 9) is the required point on curve.
OR
Using differentials, find the approximate value of \(\sqrt{49.5}\).
Solution:

Question 19.
If y = (tan-1 x)2, show that
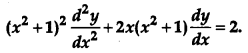 [4]
[4]
Solution:

Question 20.
Using properties of determinants, prove that
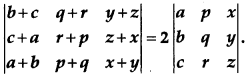 [4]
[4]
Solution:
Given,
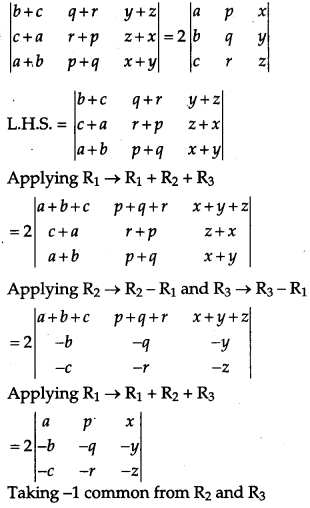
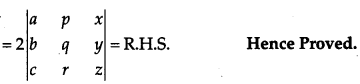
Question 21.
Prove that :
![]() [4]
[4]
Solution:
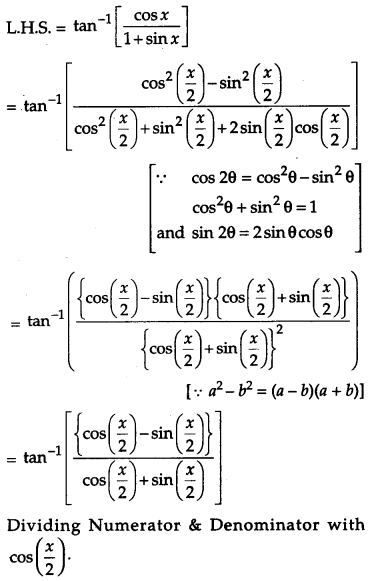
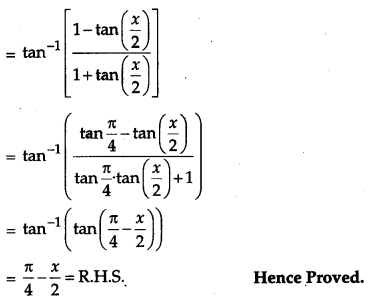
OR
Prove that
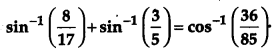
Solution:
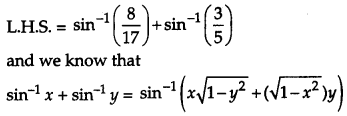
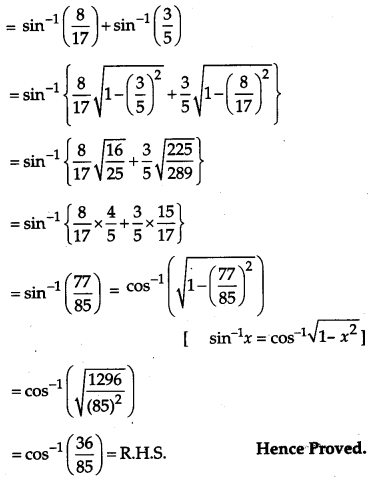
Question 22.
Let A = R – {3} and B = R – {1}. Consider the function f : A → B defined by f(x) = \(\left(\frac{x-2}{x-3}\right)\) Show that f is one-one and onto and hence find f-1. [4]
Solution:
Let x, y ϵ R such that
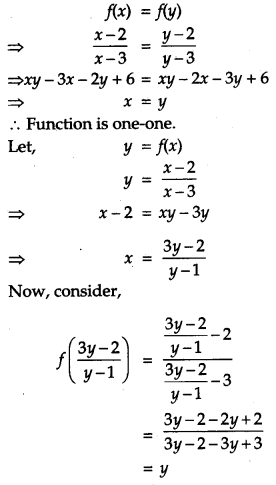

Section – C
Question 23.
Find the equation of the plane determined by the points A (3, -1, 2), B (5, 2, 4) and C (-1, -1, 6) and hence find the distance between the plane and the point P (6, 5, 9). [6]
Solution:
Any plane passes through A is,
a(x – 3) + b(y + 1) + c(z – 2) = 0 …(i)
Plane (i) passes through B and C
a(5 – 3) + (2 + 1) + c(4 – 2) = 0
⇒ 2a + 3b + 2c = 0
a(-1 – 3) + b(-1 + 1) + c(6 – 2) = 0
⇒ -4a + 4c = 0
On solving equations, we get
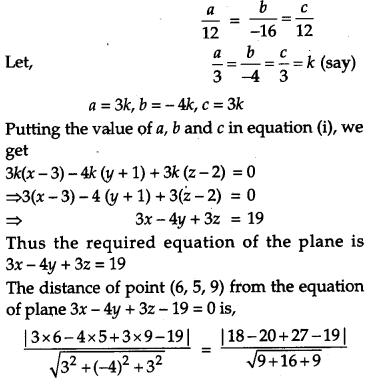
![]()
Question 24.
Of the students in a college, it is known that 60% reside in hostel and 40% are day scholars (not residing in hostel). Previous year results report that 30% of all students who reside in hostel attain’A’grade and 20% of dayscholars attain ‘A’ grade in their annual examination. At the end of the year, one student is chosen at random from the college and he has an ‘A’ grade, what is the probability that the student is a hostler ? [6]
Solution:
Let the events be defined as
E1 = Students reside in hostel
E2 = Selected student is a day scholar
A = Getting “A” grade
and P(E1) = 0.60
P(E2) = 0.40
P(A/E1) = 0.30
P(A/E2) = 0.20
We know that by Bayes’ theorem

Question 25.
A manufacturer produces nuts and bolts.lt takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts. He earns a profit of ₹ 17.50 per package on nuts and ₹ 7 per package of bolts. How many packages of each should be produced each day so as to maximize his profits if he operate his machines for at the most 12 hours a day? Form the above as a linear programming problem and solve it graphically. [6]
Solution:
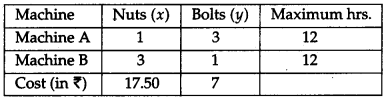
Let Packages of Nuts = x
Packages of Bolt = y
If Z denotes the total cost.
To maximise the cost, we have to maximize Z.
Maximize Z = 17.50 x + 7y
Subject to the constraints
x + 3y ≤ 12
3x + y ≤ 12
x ≥ 0, y ≥ 0
First we draw the lines AB and CD whose equations are
x + 3y = 12 …(i) 3x + y = 12 …(ii)
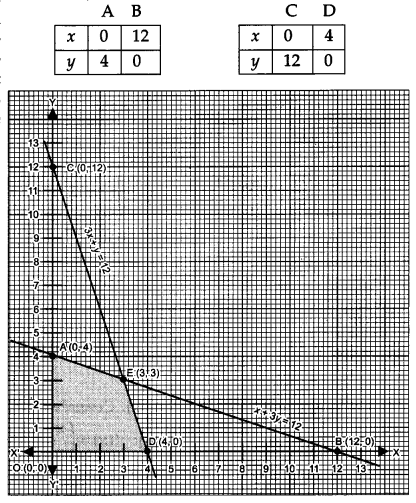
The feasible region OAEDO is shaded in the figure.
The lines are intersecting the point E(3, 3).
∴ The vertices of the feasible region are O(0, 0), A (0, 4), E (3, 3) and D(4, 0).

∴ The maximum value of Z is 73.50 at the point E(3, 3).
Hence the 3 packages of nuts and 3 packages of bolt should be produced each day to get the maximum profit of ₹ 73.50.
Question 26.
Prove that:
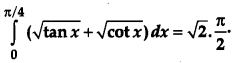 [6]
[6]
Solution:
Taking L. H. S.
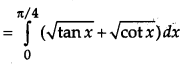
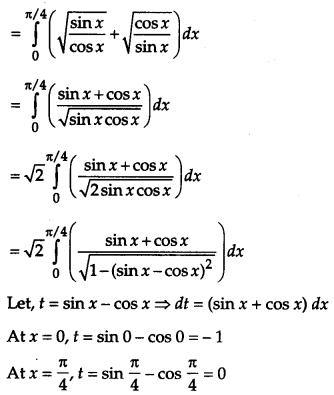
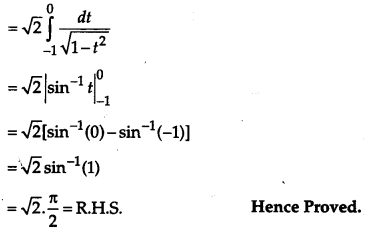
OR
Evaluate: \(\int_{1}^{3}\left(2 x^{2}+5 x\right) d x\) as a limit of a sum.
Solution:



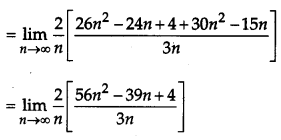
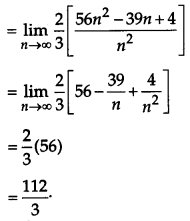
Question 27.
Using the method of integration, find the area of the region bounded by the lines 3x – 2y +1 = 0, 2x + 3y – 21 = 0 and x – 5y + 9 = 0.
Solution:
Given equations are,
3x – 2y + 1 = 0
2x + 3y – 21 = 0 .
x – 5y + 9 = 0
Taking, 3x – 2y + 1 = 0
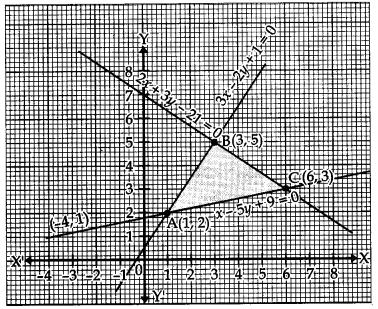
The required area of shaded bounded region ABCA = Area under line AB + Area under line BC – Area underline AC
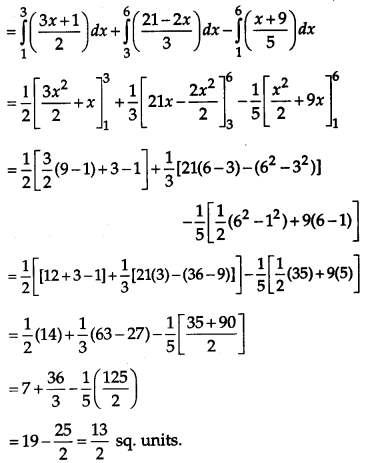
Question 28.
Show that the height of a closed right circular cylinder of given surface and maximum volume, is equal to the diameter of its base. [6]
Solution:
Let the surface area of cylinder is ‘S’ and volume is ‘V’.

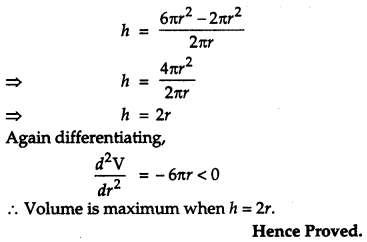
Question 29.
Using matrices, solve the following system of linear equations:
x – y + 2z =7
3x + 4y – 5z = – 5
2x -y + 3z = 12[6]
Solution:
Given equations are
x – y + 2z = 7
3x + 4y – 5z = – 5
2x – y + 3z = 12
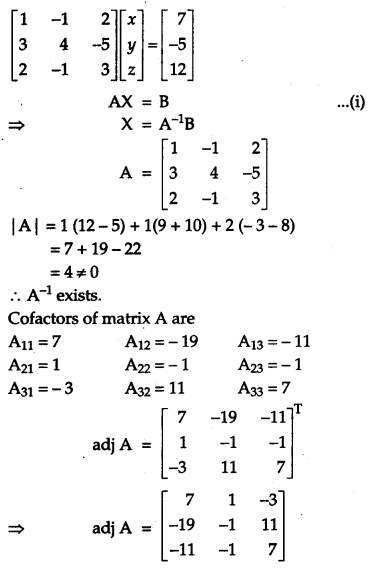
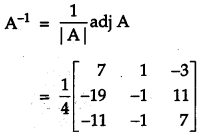
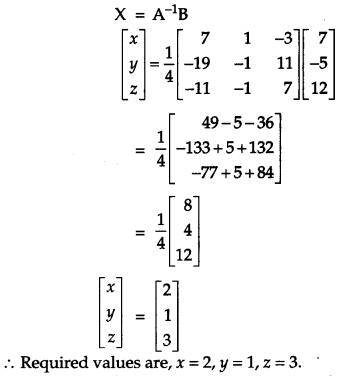
OR
Using elementary operations, find the inverse of the following matrix:
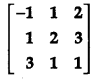
Solution:

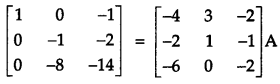

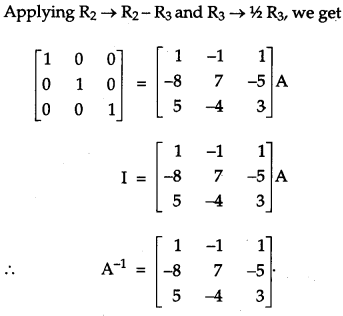
CBSE Previous Year Question Papers Class 12 Maths 2012 Delhi Set II
Note: Except for the following questions, all the remaining questions have been asked in previous set.
Section – A
Question 9.
Find the sum of the following vectors:
![]() [1]
[1]
Solution:
The given vectors are
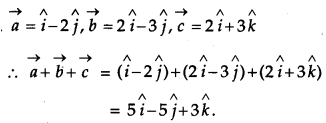
Question 10.
If ∆ = \(\left|\begin{array}{lll}{5} & {3} & {8} \\ {2} & {0} & {1} \\ {1} & {2} & {3}\end{array}\right|\) write the cofactor of the element a32. [1]
Solution:
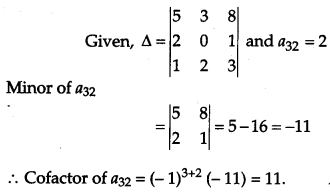
Section – B
Question 19.
Using properties of determinants, prove the following:
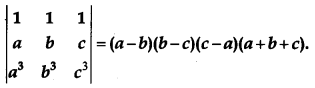 [4]
[4]
Solution:
L.H.S.

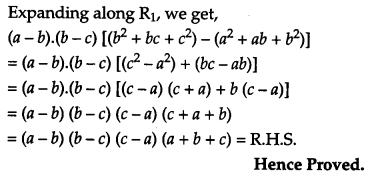
Question 20.
If y = 3 cos (log x) + 4 sin (log x), show that
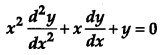 [4]
[4]
Solution:
Given, y = 3 cos (log x) + 4 sin (log x) ….(i)
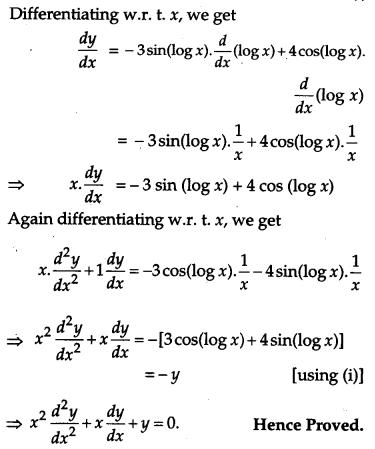
Question 21.
Find the equation of the line passing through the point (-1, 3, – 2) and perpendicular to the lines
![]() [4]
[4]
Solution:
Let a, b, c be the direction ratios of the line which is perpendicular to the lines
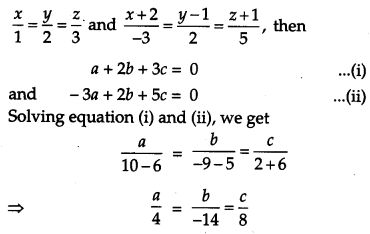
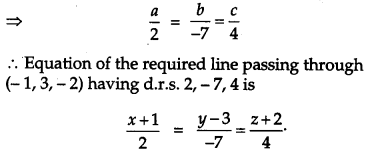
Question 22.
Find the particular solution of the following differential equation; (x + 1)\(\frac{d y}{d x}\) = 2e-y -1; y = 0 when x = 0. [4]
Solution:
The given differential equation is
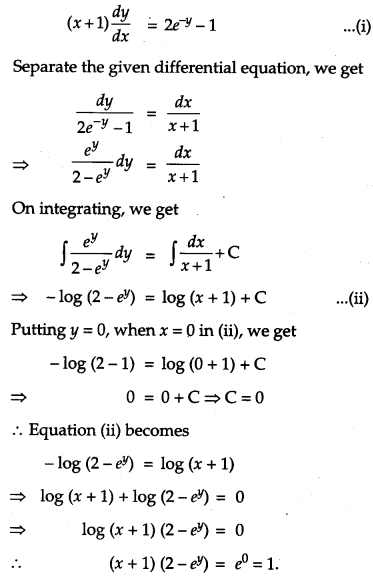
Section – C
Question 28.
A girl throws a die. If she gets a 5 or 6, she tosses a coin three times and notes the number of heads. If she gets 1, 2, 3 or 4, she tosses a coin two times and notes the number of heads obtained. If she obtained exactly two heads, what is the probability that she threw 1, 2, 3 or 4 with the die ? [6]
Solution:
Let A1 be even that the girl gets 5 or 6 and hence tosses a coin 3-times.
A1 be the even that girl gets 1, 2, 3 or 4 and hence tosses a coin 2-times.
and A be even that the girl gets exactly two heads.

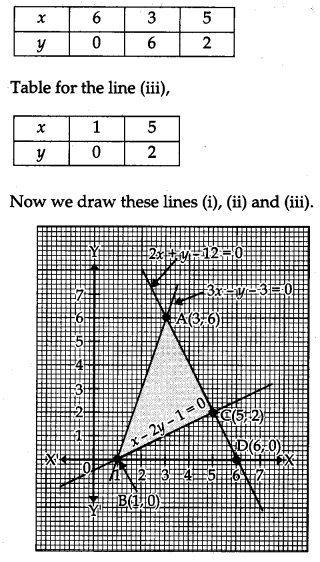
Question 29.
Using the method of integration, find the area of the region bounded by the following lines 3x – y – 3 = 0, 2x + y -12 = 0, x – 2y -1 = 0. [6]
Solution:
The given lines are

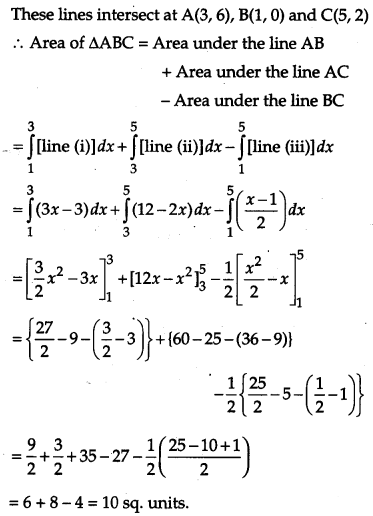
CBSE Previous Year Question Papers Class 12 Maths 2012 Delhi Set III
Note: Except for the following questions, all the remaining questions have been asked in previous sets.
Section – A
Question 9.
Find the sum of the following vectors:
![]() [1]
[1]
Solution:
The given vectors are
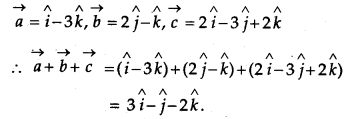
Question 10.
If ∆ = \(\left|\begin{array}{lll}{1} & {2} & {3} \\ {2} & {0} & {1} \\ {5} & {3} & {8}\end{array}\right|\), write the minor of the element a22. [1]
Solution:
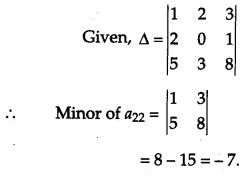
Section – B
Question 19.
Using properties of determinants, prove the following:
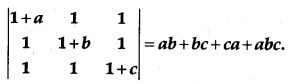 [4]
[4]
Solution:
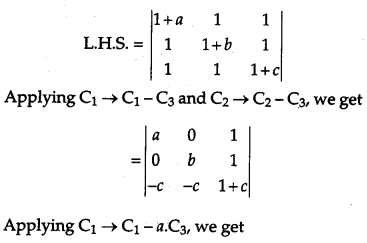
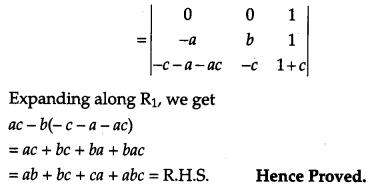
Question 20.
If y = sin-1 x, show that (1 – x2)\(\frac{d^{2} y}{d x^{2}}-x \frac{d y}{d x}\) = 0 [4]
Solution:

Question 21.
Find the particular solution of the following differential equation:
![]() [4]
[4]
Solution:
The given differential equation is
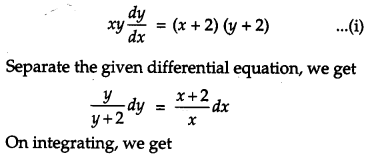
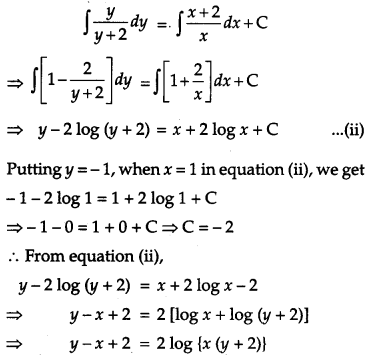
This is the required particular solution of the given differential equation.
Question 22.
Find the equation of a line passing through the point P(2, -1, 3) and perpendicular to the lines
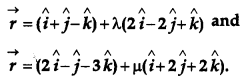 [4]
[4]
Solution:
The given lines are

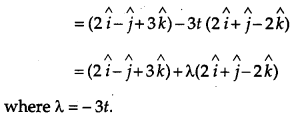
Section – C
Question 28.
Bag I contains 3 red and 4 black balls and Bag II contains 4 red and 5 black balls. Two balls are transferred at random from Bag I to Bag II and then a ball is drawn from Bag II. The ball so drawn is found to be red in colour. Find the probability that the transferred balls were both black. [6]
Solution:
Let,
E1 = Both transferred balls from bag I to bag II are red.
E2 = Both transferred balls from bag I to bag II are black.
E3 = Out of transferred balls one is black and other is red.
A = Drawing a red ball from bag II

Question 29.
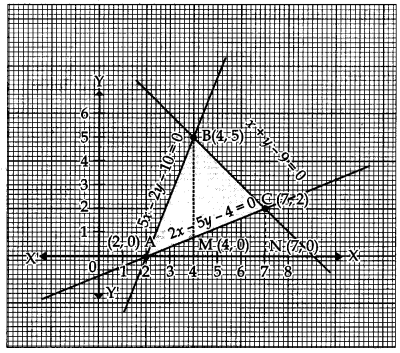
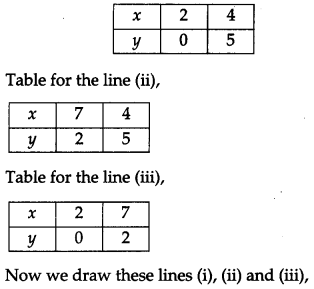
Using the method of integration, find the area of the region bounded by the following lines 5x – 2y -10 = 0, x + y – 9 = 0, 2x – 5y – 4 = 0. [6]
Solution:
The given lines are