CBSE Class 10 Maths Question Paper 2023 (Series: WX1YZ/4) with Solutions

Students can use CBSE Previous Year Question Papers Class 10 Maths with Solutions and CBSE Class 10 Maths Question Paper 2023 (Series: WX1YZ/4) to familiarize themselves with the exam format and marking scheme.

CBSE Class 10 Maths Question Paper 2023 (Series: WX1YZ/4) with Solutions

Time allowed: 3 hours
Maximum marks: 80

General Instructions:
Read the following instructions carefully and follow them:

1. This question paper contains 38 questions. All questions are compulsory.
2. Question paper is divided into FIVE Sections – Section A, B, C, D and E.
3. In Section A – Question no. 1 to 18 are Multiple Choice Questions (MCQ) and Question number 19 and 20 are Assertion-Reason based questions of 1 mark each.
4. In Section B – Question number 21 to 25 are Very Short Answer (VSA) type questions of 2 marks each.
5. In Section C – Question number 26 to 31 are Short Answer (SA) type questions, carrying 3 marks each.
6. In Section D – Question number 32 to 35 are Long Answer (LA) type questions carrying 5 marks each.
7. In Section E – Question number 36 to 38 are case study based integrated units of assessment questions
   carrying 4 marks each. Internal choice is provided in 2 mark questions in each Case-study.
8. There is no overall choice. However, an internal choice has been provided in 2 questions in Section B, 2 questions in Section C, 2 questions in Section D and 3 questions in Section E.
9. Draw neat figures wherever required. Take π = 22/7 wherever required if not stated.
10. Use of calculators is NOT allowed.

SET I Code No. 30/4/1
Section – A (Multiple choice questions)

Section A consists of Multiple Choice Type Questions of 1 Mark each.

Question 1.
The ratio of HCF to LCM of the least composite number and the least prime number is: 1
(a) 1 : 2
(b) 2 : 1
(c) 1 : 1
(d) 1 : 3
Answer:
(a) 1 : 2
Least Composite number is 4 = 2²
Least Prime number is 2 = 2¹
HCF (4, 2) is 2¹ = 2
LCM (4, 2) is 2² = 4
∴ \(\frac{\mathrm{HCF}}{\mathrm{LCM}}\) = \(\frac{2}{4}\) = \(\frac{1}{2}\) i.e., 1 : 2

Question 2.
The roots of the equation x² + 3x – 10 = 0 are: 1
(a) 2, -5
(b) -2, 5
(c) 2, 5
(d) -2, -5
Answer:
(a) 2, -5
Given, x² + 3x – 10 = 0
⇒ x² + 5x – 2x – 10 = 0
⇒ x(x + 5) -2(x + 5) = 0
⇒ (x – 2) (x + 5) = 0
Zeroes are x – 2 = 0 or x + 5 = 0
∴ x = 2 or x = -5

Question 3.
The next term of the A.P.: √6, \(\sqrt{24}\), \(\sqrt{54}\) is: 1
(a) \(\sqrt{60}\)
(b) \(\sqrt{96}\)
(c) \(\sqrt{72}\)
(d) \(\sqrt{216}\)
Answer:
(b) \(\sqrt{96}\)
√6 = \(\sqrt{1 \times 6}\) = 1√6
\(\sqrt{24}\) = \(\sqrt{4 \times 6}\) = 2√6
\(\sqrt{54}\) = \(\sqrt{9 \times 6}\) = 3√6
∴ Next term = 4√6 = \(\sqrt{4 \times 4 \times 6}\) = \(\sqrt{96}\)

Question 4.
The distance of the point (-1, 7) from x-axis is: 1
(a) -1
(b) 7
(c) 6
(d) \(\sqrt{50}\)
Answer:
(b) 7
Distance between (-1, 7) from x-axis is 7 (ordinate).

Question 5.
What is the area of a semi-circle of diameter ‘d’? 1
(a) \(\frac{1}{16}\)πd²
(b) \(\frac{1}{4}\)πd²
(c) \(\frac{1}{8}\)πd²
(d) \(\frac{1}{2}\)πd²
Answer:
(c) \(\frac{1}{8}\)πd²
Here, radius, r = \(\frac{\text { diameter }}{2}\) = \(\frac{d}{2}\) ………. (i)
∴ Area of semi-circle = \(\frac{1}{2}\)πr²
= \(\frac{1}{2}\)π(\(\frac{d}{2}\))² = (\(\frac{\pi d^2}{8}\)) ………[From (i)

Question 6.
The empirical relation between the mode, median and mean of a distribution is: 1
(a) Mode = 3 Median – 2 Mean
(b) Mode = 3 Mean – 2 Median
(c) Mode = 2 Median – 3 Mean
(d) Mode = 2 Mean – 3 Median
Answer:
(a) Mode = 3 Median – 2 Mean
As we know,
3 Median = Mode + 2 Mean
∴ Mode = 3 Median – 2 Mean

Question 7.
The pair of linear equations 2x = 5y + 6 and 15y = 6x – 18 represents two lines which are: 1
(a) intersecting
(b) parallel
(c) coincident
(d) either intersecting or parallel
Answer:
(c) coincident
Given. 2x – 5y = 6
and 6x – 15y = 18
Here, \(\frac{a_1}{a_2}\) = \(\frac{2}{6}\) = \(\frac{1}{3}\); \(\frac{b_1}{b_2}\) = \(\frac{-5}{-15}\) = \(\frac{1}{3}\); \(\frac{c_1}{c_2}\) = \(\frac{6}{18}\) = \(\frac{1}{3}\)
∴ \(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) = \(\frac{c_1}{c_2}\) = \(\frac{1}{3}\)
Hence Coincident.

Question 8.
If α, β are zeroes of the polynomial x² – 1, then value of (α + β) is: 1
(a) 2
(b) 1
(c) -1
(d) 0
Answer:
(d) 0
We have x² – 1
∴ a = 1, b = 0, c = -1 ……….. (i)
∴ Sum of zeroes, α + β = \(\frac{-b}{a}=\frac{-0}{1}\) = 0

Question 9.
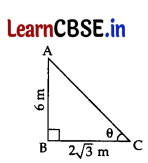
If a pole 6 m high casts a shadow 2√3 m long on the ground, then sun’s elevation is: 1
(a) 60°
(b) 45°
(c) 30°
(d) 90°
Answer:
(a) 60°
In ΔABC,
⇒ tan θ = \(\frac{\mathrm{AB}}{\mathrm{BC}}\)
⇒ tan θ = \(\frac{6}{2 \sqrt{3}}\)
⇒ tan θ = √3
⇒ tan θ = tan 60° ∴ θ = 60°

Question 10.
sec θ when expressed in terms of cot θ, is equal to: 1
(a) \(\frac{1+\cot ^2 \theta}{\cot \theta}\)
(b) \(\sqrt{1+\cot ^2 \theta}\)
(c) \(\frac{\sqrt{1+\cot ^2 \theta}}{\cot \theta}\)
(d) \(\frac{\sqrt{1-\cot ^2 \theta}}{\cot \theta}\)
Answer:
(c) \(\frac{\sqrt{1+\cot ^2 \theta}}{\cot \theta}\)
As we know, sec² θ = 1 + tan² θ
⇒ sec² θ = 1 + \(\frac{1}{\cot ^2 \theta}\) ⇒ sec² θ = \(\frac{\cot ^2 \theta+1}{\cot ^2 \theta}\)
∴ sec θ = \(\sqrt{\frac{\cot ^2 \theta+1}{\cot ^2 \theta}}\) = \(\frac{\sqrt{1+\cot ^2 \theta}}{\cot \theta}\)

Question 11.
Two dice are thrown together. The probability of getting the difference of numbers on their upper faces equals to 3 is: 1
(a) \(\frac{1}{9}\)
(b) \(\frac{2}{9}\)
(c) \(\frac{1}{6}\)
(d) \(\frac{1}{12}\)
Answer:
(c) \(\frac{1}{6}\)
Two dice can be thrown as 6 × 6 = 36 ways.
Difference of 3 can be obtained as (1, 4), (4, 1), (2, 5), (5, 2), (3, 6), (6, 3), i.e., 6 ways
∴ Required Probability = \(\frac{6}{36}\) or \(\frac{1}{6}\).

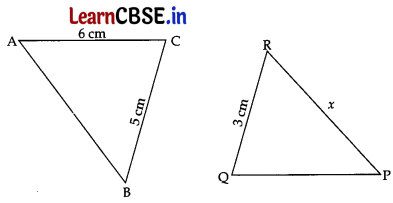
Question 12.
In the given figure, ΔABC ~ ΔQPR. If AC = 6 cm, BC = 5 cm, QR = 3 cm and PR = x; then the value of x is: 1

(a) 3.6 cm
(b) 2.5 cm
(c) 10 cm
(d) 3.2 cm
Answer:
(b) 2.5 cm
Given. AC = 6 cm, BC = 5 cm,
QR = 3 cm and PR = x
ΔABC ~ ΔQPR …[Given
∴ \(\frac{\mathrm{AC}}{\mathrm{QR}}\) = \(\frac{\mathrm{BC}}{\mathrm{PR}}\) …[CPST
⇒ \(\frac{6}{3}\) = \(\frac{5}{x}\) ⇒ 2x = 5
∴ x = \(\frac{5}{2}\) = 2.5 cm

Question 13.
The distance of the point (-6, 8) from origin is: 1
(a) 6
(b) -6
(c) 8
(d) 10
Answer:
(d) 10
Distance from the Origin
= \(\sqrt{(0+6)^2+(0-8)^2}\)
= \(\sqrt{(6)^2+(-8)^2}\) = \(\sqrt{36+64}\) = \(\sqrt{100}\)
= 10 cm

Question 14.
In the given figure, PQ is a tangent to the circle with centre O.
If ∠OPQ = x, ∠POQ = y, then x + y is: 1

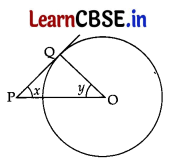
(a) 45°
(b) 90°
(c) 60°
(d) 180°
Answer:
(b) 90°

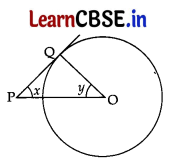
Given. OQ is the radius and PQ is the tangent
∠OQP = 90° …[Tangent is ⊥ to the radius through the point of contact
In ∆PQO, x + y + ∠OQP = 180° …[Angles-sum-property of a ∆
⇒ x + y + 90° = 180° ∴ x + y = 90°

Question 15.
In the given figure, TA is a tangent to the circle with centre O such that OT = 4 cm, ∠OTA = 30°, then length of TA is: 1

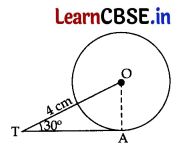
(a) 2√3 cm
(b) 2 cm
(c) 2√2 cm
(d) √3 cm
Answer:
(a) 2√3 cm
Construction: Join OA.

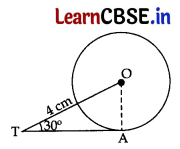
∠OAT = 90° …[Tangent is ⊥ to the the radius through point of contact
In rt. ∆OAT, cos 30° = \(\frac{\mathrm{TA}}{\mathrm{OT}}\)
⇒ \(\frac{\sqrt{3}}{2}=\frac{\mathrm{TA}}{4}\) ⇒ 2 TA = 4√3
∴ TA = 2√3 cm

Question 16.
In ΔABC, PQ || BC. If PB = 6 cm, AP = 4 cm, AQ = 8 cm, find the length of AC. 1

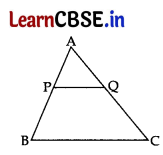
(a) 12 cm
(b) 20 cm
(c) 6 cm
(d) 14 cm
Answer:
(b) 20 cm
In ∆ABC, PQ||BC ….[Given
∴ \(\frac{\mathrm{AP}}{\mathrm{PB}}\) = \(\frac{\mathrm{AQ}}{\mathrm{QC}}\) …….[Thales Theorem
⇒ \(\frac{4}{6}\) = \(\frac{8}{\mathrm{QC}}\)
⇒ 2QC = 24 ⇒ QC = 12 cm
∴ AC = AQ + QC = 8 + 12 = 20 cm

Question 17.
If α, β are the zeroes of the polynnomial p(x) = 4x² – 3x – 7, then(\(\frac{1}{\alpha}+\frac{1}{\beta}\)) is equal to: 1
(a) \(\frac{7}{3}\)
(b) \(\frac{-7}{3}\)
(c) \(\frac{3}{7}\)
(d) \(\frac{-3}{7}\)
Answer:
(d) \(\frac{-3}{7}\)
We have 4x² – 3x – 7
∴ a = 4, b = -3, c = -7

Question 18.
A card is drawn at random from a well-shuffled pack of 52 cards. The probability that the card drawn is not an ace is: 1
(a) \(\frac{1}{13}\)
(b) \(\frac{9}{13}\)
(c) \(\frac{4}{13}\)
(d) \(\frac{12}{13}\)
Answer:
(d) \(\frac{12}{13}\)P(not an ace) = 1 – P(ace) = 1 – \(\frac{4}{52}\) = \(\frac{12}{13}\)

Assertion-Reason Based Questions
In the following questions 19 and 20, a statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct answer out of the following choices:

(a) Both (A) and (R) are true and (R) is the correct explanation of (A).
(b) Both (A) and (R) are true and (R) is not the correct explanation of (A).
(c) (A) is true and (R) is false.
(d) (A) is false, but (R) is true.

Question 19.
Assertion (A): The probability that a leap year has 53 Sundays is \(\frac{2}{7}\). 1
Reason (R): The probability that a non-leap year has 53 Sundays is \(\frac{5}{7}\).
Answer:
(c) Leap year = 366 days = 52 weeks and 2 days
Thus, a leap year always has 52 Sunday.
The remaining 2 days can be:

1. Sunday and Monday
2. Monday and Tuesday
3. Tuesday and Wednesday
4. Wednesday and Thursday,
5. Thursday and Friday
6. Friday and Saturday
7. Saturday and Sunday

Out of 7 cases, 2 have Sundays
∴ P (53 Sundays) = \(\frac{2}{7}\)
A non-leap year is composed of 365 days. There are 52 weeks and 1 day in 365 days.
As a result, there are 52 Sundays in a non-leap year. But one leftover day apart from those 52 weeks can be either a Monday, Tuesday, Wednesday, Thursday, Friday, Saturday or a Sunday.
So, P(53 Sundays in a non-leap year)
= \(\frac{1}{7}\) ≠ \(\frac{5}{7}\)
(A) is true and (R) is False

Question 20.
Assertion (A): a, b, c are in A.P. if and only if 2b = a + c. 1
Reason (R): The sum of first n odd natural numbers is n².
Answer:
(b) Assertion (A): a, b, c are in AP.
∴ b – a = c – b …[Since common difference is same 2b = a + c is true.
Reason (R): 1 + 3 + 5 + …………….. + 2n – 1
∴ S_n = \(\frac{n}{2}\)(a₁ + a_n) = \(\frac{n}{2}\)(1 + 2n – 1) = n²,
which is also True.
But it is not the correct explanation of Assertion.

Section – B

Section B consists of Very Short Answer (VSA) type of questions of 2 marks each.

Question 21.
Two numbers are in the ratio 2 : 3 and their LCM is 180. What is the HCF of these numbers? 2
Answer:
Let numbers be 2x and 3x.
Given. LCM (2x, 3x) is 6x
⇒ 6x = 180 ⇒ x = 30
∴ HCF (2x, 3x) is x = 30

Question 22.
If one zero of the polynomial p(x) = 6x² + 37x – (k – 2) is reciprocal of the other, then find the value of k. 2
Answer:
Given. 6x² + 37x – (k – 2)
∴ a = 6, 6 = 37, c = -(k- 2)
Let zeroes be and \(\frac{1}{\alpha}\).
Product of zeroes = \(\frac{\text { constant term }}{\text { coefficient of } x^2}=\frac{c}{a}\)
α × \(\frac{1}{\alpha}=\frac{-(k-2)}{6}\)
⇒ 1 = \(\frac{-k+2}{6}\)
⇒ 6 = -k + 2
∴ k = 2 – 6 = -4

Question 23.
(A) Find the sum and product of the roots of the quadratic equation 2x² – 9x + 4 = 0. 2
Or
(B) Find the discriminant of the quadratic equation 4×2 -5 = 0 and hence comment on the nature of roots of the equation. 2
Answer:
(A) Given. 2x² – 9x + 4 = 0
Here a = 2, b = -9, c = 4
∴ Sum of roots = \(\frac{-b}{a}=\frac{-(-9)}{2}=\frac{9}{2}\)
and Product of roots = \(\frac{c}{a}=\frac{4}{2}\) = 2
Or
(B) Given. 4x² – 5 = 0
Here a = 4, b = 0, c = -5
As we know, D = b² – 4ac
= (0)² – 4(4) (-5)
= 80 > 0
∴ Roots are real and unequal.

Question 24.
If a fair coin is tossed twice, find the probability of getting ‘at most one head’. 2
Answer:
S = {HH, HT, TH, TT} = 4
Atmost 1 head, HT, TH, TT i.e., 3
∴ P(atmost 1 head) = \(\frac{3}{4}\)

Question 25.
(A) Evaluate: \(\frac{5 \cos ^2 60^{\circ}+4 \sec ^2 30^{\circ}-\tan ^2 45^{\circ}}{\sin ^2 30^{\circ}+\cos ^2 30^{\circ}}\)
(Or)
(B) If A and B are acute angles such that sin(A – B) = 0 and 2cos(A + B) – 1 = 0, then find angles A and B. 2
Answer:

Or
(B) Given, sin (A – B) = 0
⇒ sin (A – B) = sin 0
⇒ A – B = 0
⇒ A = B ……..(i)
and 2 cos (A + B) – 1 = 0 …….[Given
⇒ cos (A + B) = \(\frac{1}{2}\)
⇒ cos (A + B) = cos 60°
⇒ A + B = 60°
⇒ A + A = 60° …….[From (i)
⇒ 2A = 60° ⇒ A = \(\frac{60^{\circ}}{2}\) = 30°
∴ A = B = 30°

Section – C

Section C consists of Short Answer (SA) type questions of 3 marks each.

Question 26.
(A) How many terms are there in an A.P. whose first and fifth terms are -14 and 2, reespectively and the last term is 62. 3
Or
(B) Which term of the A.P.: 65, 61, 57, 53, ……………. is the first negative term? 3
Answer:
(A) Given. 1^st term, a = -14, a₅ = 2 and a_n = 62
a₅ = a + 4d
⇒ -14 + 4d = 2 ⇒ 4d = 16
∴ d = \(\frac{16}{4}\) = 4 ……………(i)
Now, a_n = 62
⇒ a +(n – 1 )d = 62
⇒ -14 +(n – 1)4 = 62
⇒ (n – 1)4 = 62 + 14
⇒ (n – 1) = \(\frac{76}{4}\) = 19
⇒ n = 19 + 1 = 20
∴ Numbers of terms, n = 20
Or
(B) a = 65, d = 61 – 65 = -4
a_n < 0 …[First negative term
⇒ a + (n – 1 )d < 0
⇒ 65 + (n – 1) (-4) < 0
⇒ 65 < 4 (n – 1)
⇒ \(\frac{65}{4}\) < n – 1 ⇒ \(\frac{65}{4}\) + 1 < n
⇒ \(\frac{65+4}{4}\) < n ∴ n > \(\frac{69}{4}\) or 17.75
Hence First negative term is 18^th term.

Question 27.
Prove that √5 is an irrational number. 3
Answer:
Let us assume, to the contrary, that √5 is rational.
So, we can find integers p and q (q ≠ 0)
Such that √5 = \(\frac{p}{q}\), where p and q are coprime.
Squaring both sides, we get
5 = \(\frac{p^2}{q^2}\) ⇒ 5q² = p² …… (i)
∴ 5 divides p². ⇒ 5 divides p
So, let p = 5r
Putting the value of p in (i), we get
5q² = (5r)² => 5q² = 25r²
⇒ q² = 5r²
∴ 5 divides q² ⇒ 5 divides q.
∴ p and q have atleast 5 as a common factor.
But this contradicts the fact that p and q have no common factor.
So, our assumption is wrong.
∴ √5 is irrational. (Hence Proved)

Question 28.
Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre. 3
Answer:
Given. PA and PB are two tangent from P which make ∠APB.
To Prove. ∠1 + ∠3 = 180°
Proof. ∠2 = 90° …….. (i)
∠4 = 90° ………. (ii)
…… [Tangent is⊥to the radius through the point of contact

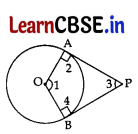
In Quadrilateral OAPB,
∴ ∠1 + ∠2 + ∠3 + ∠4 = 360°
…[Sum of all angles of a Quadrilateral is 360°
∠1 + 90° + ∠3 + 90° = 360° ……[From (i) & (ii)
∴ ∠1 + ∠3 = 360° – 180°
= 180° (Hence Proved)

Question 29.
(A) Prove that: \(\frac{\sin A-2 \sin ^3 A}{2 \cos ^3 A-\cos A}\) = tan A 3
Or
(B) Prove that: sec A (1 – sin A) (sec A + tan A) = 1. 3
Answer:

Or

Question 30.
Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle. 3
Answer:

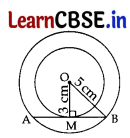
∠OMB = 90° …[∵ Tangent is⊥to the radius through the point of contact.
In rt. ΔOMB,
OM² + MB² = OB²
…[Pythagoras’ theorem
(3)² + (MB)² = (5)²
⇒ 9 + (MB)² = 25
⇒ MB² = 25 – 9 = 16 ⇒ MB = +4 cm
Here, AM = MB = 4 cm …[∵ ⊥ from the centre bisects the chord
∴ AB = AM + MB = 4 + 4 = 8 cm

Question 31.
Find the value of ‘p’ for which the quadratic equation px(x – 2) + 6 = 0 has two equal real roots. 3
Answer:
We have, px (x – 2) + 6 = 0
⇒ px² – 2px + 6 = 0, p ≠ 0
For two equal roots, …[Given
∴ b² – 4ac = 0 (a = p, b = -2p, c = 6)
⇒ (-2p)² – 4 (P)(6) = 0
⇒ 4p² – 24p = 0 ⇒ 4p(p – 6) = 0
⇒ 4p = 0 or p – 6 = 0
p = 0 or p = 6
But p ≠ 0 Standard form of a quad. eq”. ax² + bx + c = 0, a ≠ 0
∴ P = 6

Section – D

Section D consists of Long Answer (LA) type questions of 5 marks each.

Question 32.
(A) A straight highway leads to the foot of a tower. A man standing on the top of the 75 m high tower observes two cars at angles of depression of 30° and 60°, which are approaching the foot of the tower. If one car is exactly behind the other on the same side of the tower, find the distance between the two cars, (use √3 = 1.73) 5
Or
(B) From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 30°. Determine the height of the tower. 5
Answer:
(A) Let AB be the tower.
C and D be the two cars.

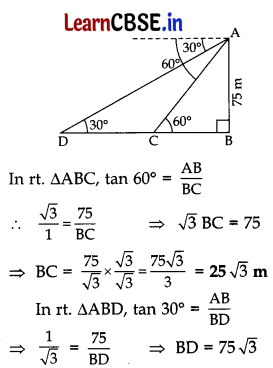
∴ Distance between two cars,
CD = BD – BC
= 75√3 – 25√3 = 50√3m
= 50(1.73) …[∵ √3 = 1.73 (Given)
= 86.5 m
Or
(B) Let AB be the building and EC be the cable tower.

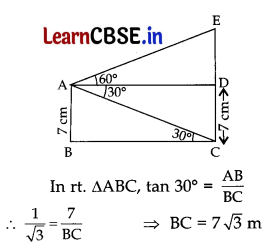
Here, AD = BC = 7√3 m
In rt. ΔADE, tan 60° = \(\frac{\mathrm{DE}}{\mathrm{AD}}\)
∴ \(\frac{\sqrt{3}}{1}=\frac{D E}{7 \sqrt{3}}\) ⇒ DE = 21 m
∴ Height of cable tower, CE = CD + DE
= 7 + 21 …[∵ CD = AB = 7m
= 28 m

Question 33.
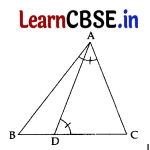
(A) D is a point on the side BC of a triangle ABC such that ∠ADC = ∠BAC, prove that CA² = CB.CD. 5
Or
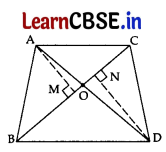
(B) If AD & PM are medians of triangles ABC and PQR, respectively where ΔABC ~ ΔPQR, prove: \(\frac{\mathrm{AB}}{\mathrm{PQ}}\) = \(\frac{\mathrm{AD}}{\mathrm{PM}}\). 5
Answer:
(A) Given: D is a point on the side BC of a ΔABC such that ∠ADC = ∠BAC.
To prove:
CA² = CB.CD
Proof: In ΔABC and ΔDAC,
∠BAC = ∠ADC …[Given
∠C = ∠C …[Common
∴ ∠ABC = ∠DAC …[3^rd angle
∴ ΔABC ~ ADAC
∴ \(\frac{\mathrm{BC}}{\mathrm{AC}}\) = \(\frac{\mathrm{AC}}{\mathrm{DC}}\) …[In similar Δs Corresponding sides are proportional
⇒ AC² = CB.CD (Hence Proved)

Or

Question 34.
A student was asked to make a model shaped like a cylinder with two cones attached to its ends by using a thin aluminium sheet. The diameter of the model is 3 cm and its total length is 12 cm. If each cone has a height of 2 cm, find the volume of air contained in the model. 5
Answer:
Let H be the height of cylinder and h be the height of cones respectively.

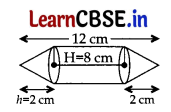
r be the common radius for cylinder as . well as for cones.
∴ H = 12 – 2 – 2 = 8 cm, h = 2 cm, r = \(\frac{3}{2}\) cm.
Volume of air contained in the model = Vol. of cyl. + 2(Vol. of cone)
= πr²H + 2(\(\frac{1}{3}\)πr²h) = πr²(H + \(\frac{1}{3}\)h)
\(\frac{22}{7}\) × \(\frac{3}{2}\) × \(\frac{3}{2}\) [8 + \(\frac{2}{3}\) × 2
= \(\frac{99}{14}\) × (\(\frac{24+4}{3}\)) = \(\frac{33}{14}\) × 28 = 66 cm³

Question 35.
The monthly expenditure on milk in OO families of a Housing Society is given below: 5

Find the value of x and also, find the median and mean expenditure on milk.
Answer:

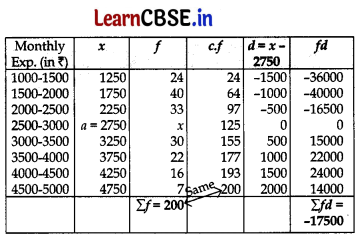
Given. Σf = 200
24 + 40 + 33 + x + 30 + 22 + 16 + 7 = 200
⇒ 172 + x = 200 ∴ x = 200 – 172 = 28
Here, = \(\frac{n}{2}=\frac{200}{2}\) = 100
∴ Median Class is 2500 – 3000
∴ Median = l + \(\frac{\frac{n}{2}-c . f .}{f}\) × h [… l = 2500, c.f = 97, f = 28, h = 500
= 2500 + (\(\frac{100-97}{28}\) × 500)
= 2500 + \(\frac{3 \times 500}{28}\) = 2500 + \(\frac{375}{7}\)
= 2500 + 53.57
= ₹2553.57 (approx.)
Now Mean = a + \(\frac{\Sigma f d}{\Sigma f}\) = 2750 + \(\frac{(-17500)}{200}\)
= 2750 – 87.50 = ₹2662.50

Section – E

Section E consists of three Case Study Based questions of 4 marks each.

Question 36.
Two schools ‘P’ and ‘Q’ decided to award prizes to their students for two games of Hockey ₹x per student and Cricket ₹y per student. School ‘P’ decided to award a total of ₹9,500 for the two games to 5 and 4 students respectively; while school ‘Q’ decided to award ₹7,370 for the two games to 4 and 3 students respectively.

Based on the above information, answer the following questions:
(i) Represent the given information algebraically (in terms of x and y). 1
(ii) (a) What is the prize amount for hockey? 2
Or
(b) Prize amount on which game is more and by how much? 2
(iii) What will be the total prize amount if there are 2 students each from two games? 1
Answer:
(i) School P : 5x + 4y = ₹9500 ………… (i)
School Q : 4x + 3y = ₹7370 …………….. (ii)
(ii) (a) Multiplying (i) by 3 and (ii) by 4 and subtracting, we get

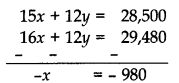
∴ x (Prize amount for Hockey) = ₹980
Or
(b) Putting the value of x in (i);
5(980) + 4y = 9500
⇒ 4900 + 4y = 9500
⇒ 4y = 9500 – 4900
⇒ y = \(\frac{4600}{4}\) = ₹1150
∴ Prize amount of circket is more than Hockey Prize.
Difference = y – x
= ₹1150 – 980 = ₹170

(iii) Total prize would be = 2x + 2y
= 2(x + y)
= 2(980 + 1150) = 2(2130)
= ₹4260

Question 37.
Jagdish has a field which is in the shape of a right angled trainagle AQC. He wants to leave a space in the form of a square PQRS inside the field for growing wheat and the remaining for growing vegetables (as shown in the figure).
In the field, there is a pole marked as O.

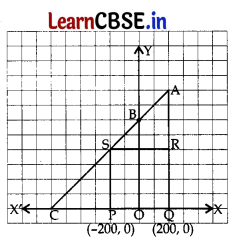
Based on the above information, answer the following questions:
(i) Taking O as origin, coordinates of P are (-200, 0) and of Q are (200, 0). PQRS being a square, what are the coordinates of R and S? 1
(ii) (a) What is the area of square PQRS? 2
Or
(b) What is the length of diagonal PR in square PQRS? 2
(iii) If S divides CA in the ratio K : 1, what is the value of K, where point A is (200, 800)? 1
Answer:

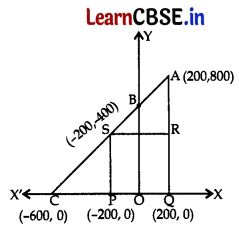
(i) Coordinates of R(200, 400)
S(-200, 400)

(ii) (a) Area of Square, PQRS = side × side
= 400 × 400
= 1,60,000 sq. units
Or
(b) Diagonal of a square = side √2
= 400 √2 units.
Alternatively,
By Using pythagoras’ theorem, we have
PR² = PQ² + QR²
⇒ PR² = (400)² + (400)²
⇒ PR² = 160000 + 160000
PR = \(\sqrt{320000}\) = \(\sqrt{4 \times 4 \times 2 \times 100 \times 100}\)
= 4 × 100√2 = 400 √2 units

(iii)

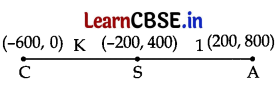
Coordinates of S = Coordinates of S
∴ (\(\left.\frac{200 \mathrm{~K}-600}{\mathrm{~K}+1}, \frac{800 \mathrm{~K}+0}{\mathrm{~K}+1}\right)\)) = (-200, 400)
….[using section formula
\(\frac{800 \mathrm{~K}}{\mathrm{~K}+1}[latex] = 400
⇒ 800 K = 400 K + 400
⇒ 400 K = 400 ∴ K = 1

Question 38.
Governing council of a local public development authority of Dehradun decided to build an adventurous playground on the top of a hill, which will have adequate space for parking.
After survey, it was decided to build rectangular playground, with a semi-circular area allotted for parking at one end of the playground. The length and breadth of the rectangular playground are 14 units and 7 units, respectively. There are two quadrants of radius 2 units on one side for special seats.

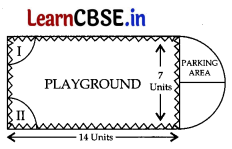
Based on the above information, answer the following questions:
(i) What is the total perimeter of the parking area? 1
(ii) (a) What is the total area of parking and the two quadrants? 2
Or
(b) What is the ratio of area of playground to the area of parking area? 2
(iii) Find the cost of fencing the playground and parking area at the rate of 2 per unit. 1
Answer:

(iii) Perimeter of playground and parking
= 7 + 14 + 14 + πr
= 35 + [latex]\frac{22}{7}\) × \(\frac{7}{2}\) = 35 + 11 = 46 units
∴ Total cost of fencing = 46 × ₹2 = ₹92

SET II Code No. 30/4/2

Note: Except for the following questions, all the remaining questions have been asked in Set – I.

Section – A

Question 1.
Which of the following is true for all values of θ (0° < θ < 90°)? 1
(a) cos² θ – sin² θ = 1
(b) cosec² θ – sec² θ = 1
(c) sec² θ – tan² θ = 1
(d) cot² θ – tan² θ = 1
Answer:
(c) sec² θ – tan² θ = 1
Identity : sec² θ = 1 + tan² θ
∴ sec² θ – tan² θ = 1

Question 2.
+If k + 2, 4k – 6 and 3k – 2 are three consecutive terms of an A.P., then the value of k is: 1
(a) 3
(b) -3
(c) 4
(d) -4
Answer:
(a) 3
k + 2, 4k – 6, 3k – 2 are in A.P.
∴ 4k – 6 – (k + 2) = 3k – 2 – (4k – 6)
⇒ 4k – 6 – k – 2 = 3k – 2 – 4k + 6 …[Common difference is same
⇒ 3k – 8 = -k + 4 ⇒ 3k + k = 4 + 8
⇒ 4k = 12 ∴ k = \(\frac{12}{4}\) = 3

Question 11.
For the following distribution: 1

The sum of lower limits of median class and modal class is:
(a) 15
(b) 25
(c) 30
(d) 35
Answer:
(a) 15

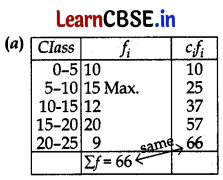
Here, \(\frac{n}{2}\) = \(\frac{66}{2}\) = 33
∴ Median Class is 10 – 15.
⇒ Lower limit of Median Class = 10
Since Maximum frequency is 15
∴ Modal Class 5 – 10.
Lower limit of Modal Class = 5
∴ Required Sum = 10 + 5 = 15

Question 12.
The length of tangent drawn to a circle of radius 9 cm from a point 41 cm from the centre is: 1
(a) 40 cm
(b) 9 cm
(c) 41 cm
(d) 50 cm
Answer:
(a) 40 cm

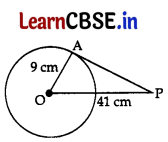
∠OAP = 90° …[∵ Tangent is ⊥ to the radius through the point of contact
In ΔOAP, OA² + AP² = OP² …[Pythagoras’ theorem
⇒ 9² + AP² = 41²
⇒ AP² = 41² – 9²
⇒ AP² = 1681 – 81 = 1600
∴ AP = \(\sqrt{1600}\) = 40 cm

Question 13.
In the given figure, O is the centre of the circle and PQ is the chord. If the tangent PR at P makes an angle of 50° with PQ, then the measure of ∠POQ is: 1

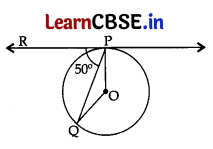
(a) 50°
(b) 40°
(c) 100°
(d) 130°
Answer:
(c) 100°

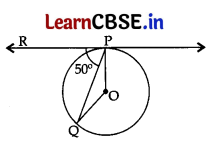
Here, ∠OPR = 900 …[∵ Tangent is⊥to the radius through the point of contact
∴ ∠RPQ + ∠OPQ = 90°
⇒ ∠OPQ = 90° – 50° = 40°
In ΔPOQ, OP = OQ …[Radii
∠OPQ = ∠PQO = 40° …[Angles opposite to equal sides are equal
In ΔPOQ, ∠QPO + ∠PQO + ∠POQ = 180° …[Angle-sum-Property of a Δ
⇒ 40° + 40° + ∠POQ = 180°
∴ ∠POQ = 180° – 80° = 100°

Question 14.
A bag contains 5 red balls and n green balls. If the probability of drawing a green ball is three times that of a red ball, then the value of n is:
(a) 18
(b) 15
(c) 10
(d) 20
Answer:
(b) 15
Total Balls = 5 + n
p(Green ball) = 3[p(Red ball)] …[given
∴ \(\frac{n}{5+n}\) = 3[latex]\frac{2}{5+n}[/latex] ⇒ n = 5
n = 15

Question 18.
The distance of the point (-1, 7) from x-axis is:
(a) -1
(b) 7
(c) 6
(d) \(\sqrt{50}\)
Answer:
(b) 7
The distance between (-1, 7) from x-axis is 7(ordinate).

Section – B

Question 21.
(A) Evaluate: \(\frac{5}{\cot ^2 30^{\circ}}+\frac{1}{\sin ^2 60^{\circ}}\) = cot² 45°+ 2sin² 90° 2
Or
(B) If θ is an acute angle and sin θ = cos θ, find the value of tan² θ + cot² θ – 2. 2
Answer:
(a) Given. \(\frac{5}{\cot ^2 30^{\circ}}+\frac{1}{\sin ^2 60^{\circ}}\) – cot² 45° + 2 sin² 90°
⇒ 5tan² 30° + cosec² 60° – (1)² + 2(1)²
⇒ 5(\(\frac{1}{\sqrt{3}}\))² + (\(\frac{2}{\sqrt{3}}\))² – 1 + 2 ⇒ \(\frac{5}{3}\) + \(\frac{4}{3}\) + 1
\(\frac{5+4+3}{3}\) = \(\frac{12}{3}\) = 4
Or
(b) Given, sin θ = cos θ
⇒ \(\frac{\sin \theta}{\cos \theta}\) = 1 ⇒ tan θ = 1
Then, cot θ = \(\frac{1}{\tan \theta}\) = \(\frac{1}{1}\) = 1
Now, tan² θ + cot² θ – 2 = (1)² + (1)² – 2
= 2 – 2 = 0

Section – C

Question 29.
(A) The sum of first 15 terms of an A.P. is 750 and its first term is 15. Find its 20^th term. 3
Or
(B) Rohan repays his total loan of ₹1,18,000 by paying every month starting with the first instalment of ₹1,000. If he increases the instalment by ₹100 every month, what amount will be paid by him in the 30^th instalment? What amount of loan has he paid after 30^th instalment? 3
Answer:
(A) Given, a = 15 and S₁₅ = 750
As we know, S_n = \(\frac{n}{2}\) [2a + (n + 1 )d]
∴ 750 = \(\frac{15}{2}\)[2(15) + (15 – 1 )d]
⇒ 30 + 14d = 750 × \(\frac{2}{15}\) ⇒ 14d = 100 – 30
⇒ d = \(\frac{70}{14}\) = 5
∴ a₂₀ = a + 19d ….[a_n = a + (n – 1)d
= 15 + 19(5)
= 15 + 95 = 110
Or
(B) Amount paid in 30 instalments
= 1000 + 1100 + 1200 + ……(30 terms)
∴ S_n = \(\frac{n}{2}\)[2a + (n – 1)d] …[a = 1000, d = 100, n = 30
= \(\frac{30}{2}\) (2000 + 29 × 100)
= 15(2000 + 2900)
= 15(4900)
= ₹73,500
∴ Amount of loan he has to pay after the 30th instalment = 1,18,000 – 73,500 = ₹44,500

Question 30.
Prove that √3 is an irrational number. 3
Answer:
Let us assume, to the contrary, that √3 is rational.
So, we can find integers p and q (q ≠ 0),
such that √3 = \(\frac{p}{q}\) where p and q are coprime.
Squaring both sides, we get
3 = \(\frac{p^2}{q^2}\)
⇒ 3 q² = p² …………. (i)
∴ 3 divides p²
⇒ 3 divides p
So, let p = 3 r
Putting the value of p in (i), we get
3q² = (3r)²
⇒ 3q² = 9r² ⇒ q² – 3r²
∴ 3 divides p²
⇒ 3 divides p
∴ 3 divides q²
⇒ 3 divides q
∴ p & q have atleast 3 as a common factor. But this contradicts the fact that p and q have no common factor. So, our assumption is wrong
∴ √3 is irrational.

Section – D

Question 32.
From a solid cylinder of height 20 cm and diameter 12 cm, a conical cavity of height 8 cm and radius 6 cm is hallowed out. Find the total surface area of the remaining solid. 5
Answer:

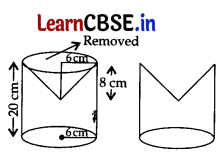
Here r = 6 cm
Height of the cylinder, H = 20 cm
Height of the cone, h = 8 cm
Slant height of cone, l = \(\sqrt{r^2+h^2}\)
= \(\sqrt{6^2+8^2}\)
= \(\sqrt{36+64}\) = \(\sqrt{100}\)
= 10 cm
∴ Total Surface Area of the remaining solid
= ar. (Cylinder + Base + cone)
= 2πrH + πr² + πrl
= πr (2H + r + l)
= \(\frac{22}{7}\) × 6 (2(20) + 6 + 10)
= \(\frac{22}{7}\) × 6 × 56 = 1056 cm²

Question 35.
(A) In the given figure, ∠ADC = ∠BCA; prove that ΔACB ~ ΔADC
Hence find BD if AC = 8 cm and AD = 3, cm. 5

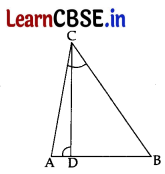
Or
(B) If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then prove that the other two sides are divided in the same ratio. 5
Answer:
(A)

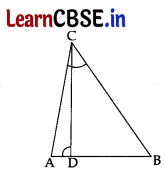
Proof: In ΔACB and ΔADC,
∠CAB = ∠DAC …[Common
∠BCA = ∠ADC …[Given
∴ ΔACB ~ ΔADC ….[AA similarly criterion
∴ \(\frac{\mathrm{AC}}{\mathrm{AD}}\) = \(\frac{\mathrm{AB}}{\mathrm{AC}}\)
⇒ \(\frac{8}{3}=\frac{A B}{8}\)
⇒ 3AB = 64 ⇒ AB = \(\frac{64}{3}\)
Now, BD = AB – AD
= \(\frac{64}{3}\) – 3 = \(\frac{64-9}{3}\) = \(\frac{55}{3}\)
∴ BD = 18.\(\overline{3}\) or 18\(\frac{1}{3}\) cm

(B) Given. In ΔABC, DE || BC
To prove: \(\frac{\mathrm{AD}}{\mathrm{DB}}\) = \(\frac{\mathrm{AE}}{\mathrm{EC}}\)
Const.: Draw EM⊥AD and DN⊥AE. Join BE and CD.

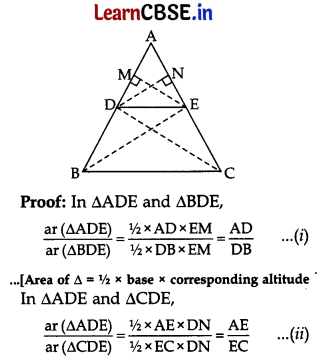
DE || BC …..[Given
∴ ar(ΔBDE) = ar(ΔCDE) ……(iii)
……[∵ Δs on the same base and between the same parallel sides are equal in area
From (i), (ii) and (iii) = \(\frac{\mathrm{AD}}{\mathrm{DB}}\) = \(\frac{\mathrm{AE}}{\mathrm{EC}}\)
Hence Proved.

SET III Code No. 30/4/3

Note: Except for the following questions, all the remaining questions have been asked in Set – I & Set II.

Section – A

Question 7.
The next term of the A.P.: √7, \(\sqrt{28}\), \(\sqrt{63}\) is : 1
(a) \(\sqrt{70}\)
(b) \(\sqrt{80}\)
(c) \(\sqrt{97}\)
(d) \(\sqrt{112}\)
Answer:
(d) \(\sqrt{112}\)
a₁ = \(\sqrt{7 \times 1}\) = 1√7
a₂ = \(\sqrt{28}\) = \(\sqrt{4 \times 7}\) = 2√7
a₃ = \(\sqrt{63}\) = \(\sqrt{9 \times 7}\) =3√7
∴ a₄ = 4^th term
= 4√7
= \(\sqrt{4 \times 4 \times 7}\)
= \(\sqrt{112}\)

Question 8.
(sec² θ – 1) (cosec² θ – 1) is equal to: 1
(a) -1
(b) 1
(c) 0
(d) 2
Answer:
(b) 1
We have (sec² θ – 1)(cosec² θ – 1)
= tan² θ.cot² θ
= tan² θ \(\frac{1}{\tan ^2 \theta}\) = 1

Question 15.
For the following distribution: 1

The modal class is:
(a) 10 – 20
(b) 20 – 30
(c) 30 – 40
(d) 50 – 60
Answer:
(c) 30 – 40

Marks	c.f.	C.I.	f
Below 10	3	0 – 10	3
Below 20	12	10 – 20	9
Below 30	27	20 – 30	15
Below 40	57	30 – 40	30 (Maximum)
Below 50	75	40 – 50	18
Below 60	80	50 – 60	5

∴ Model Class is 30 – 40.

Question 16.
In the given figure, PT is a tangent at T to the circle with centre O. If ∠TPO = 25°, then x is equal to: 1

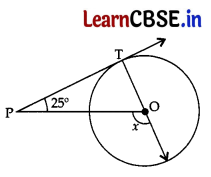
(a) 25°
(b) 65°
(c) 90°
(d) 115°
Answer:
(d) 115°

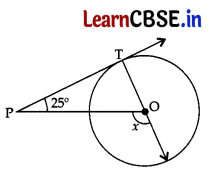
∠PTO = 90° …[∵ Tangent is⊥to the radius through the point of contact
Here, x = ∠TPO + ∠PTO …[Exterior angle theorem
∴ x = 25° + 90° = 115°

Question 17.
In the given figure, PQ || AC. If BP = 4 cm, AP = 2.4 cm and BQ = 5 cm, then length of BC is: 1

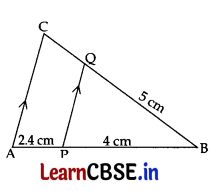
(a) 8 cm
(b) 3 cm
(c) 0.3 cm
(d) \(\frac{25}{3}\) cm
Answer:
(a) 8 cm

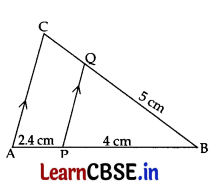
∠In ΔABC, PQ || AC …[Given
∴ \(\frac{\mathrm{BP}}{\mathrm{PA}}\) = \(\frac{\mathrm{BQ}}{\mathrm{QC}}\) …[Thales’ theorem
⇒ \(\frac{4}{2.4}=\frac{5}{\mathrm{QC}}\)
⇒ 4QC = 12
⇒ QC = 3 cm
Now, BC = BQ + QC
= 5 + 3 = 8 cm

Question 18.
The points (-4, 0), (4, 0) and (0, 3) are the vertices of a: 1
(a) right triangle
(b) isosceles triangle
(c) equilateral triangle
(d) scalene triangle
Answer:
(b) isosceles triangle
Let A(-4, 0), B(4, 0) and C(0, 3)
AB = \(\sqrt{(4+4)^2+(0-0)^2}\) = \(\sqrt{64}\) = 8 units
BC = \(\sqrt{(0-4)^2+(3-0)^2}\) = \(\sqrt{16+9}\) = \(\sqrt{25}\) = 5 units
AC = \(\sqrt{(0+4)^2+(3-0)^2}\) = \(\sqrt{16+9}\) = 5 units
Here, BC = AC
∴ ΔABC is an isosceles Δ.

Section – B

Question 22.
(A) Evaluate: 2 sec2 θ + 3 cosec2 θ – 2 sin θ cos θ if θ = 45°. 2
Or
(B) If sin θ – cos θ = 0, then find the value of sin⁴ θ + cos⁴ θ. 2
Answer:
(A) 2 sec² θ + 3 cosec² θ – 2 sin θ cos θ
= 2sec² 45° + 3 cosec² 45° – 2 sin 45° cos 45°
= 2(√2)² + 3(√2)² – 2(\(\frac{1}{\sqrt{2}}\))(\(\frac{1}{\sqrt{2}}\))
= 2(2) + 3(2) – 1
= 4 + 6 – 1 = 9
Or
(B) Given, sin θ – cos θ = 0
⇒ sin θ = cos θ
⇒ \(\frac{\sin \theta}{\cos \theta}\) = 1
⇒ tan 0 = tan 45°
∴ θ = 45° ………… (i)
Now, sin⁴ θ + cos⁴ θ
(sin 45°)⁴ + (cos 45°)⁴ …[From (i)
= (\(\frac{1}{\sqrt{2}}\))⁴ + (\(\frac{1}{\sqrt{2}}\))⁴
= \(\frac{1}{4}\) + \(\frac{1}{4}\) = \(\frac{2}{4}\) = \(\frac{1}{2}\)

Section – C

Question 26.
Find the value of ‘p’ for which one root of the quadratic equation px² – 14x + 8 = 0 is 6 times the other. 3
Answer:
Given, px² – 14x + 8 = 0
Let roots be α and 6α.
Here, a = p, b = -14, c = 8
Sum of roots = \(\frac{-b}{a}\)
∴ α + 6α = \(\frac{-(-14)}{p}\)
⇒ 7α = \(\frac{14}{p}\)
⇒ α = \(\frac{2}{p}\)
Product of roots = \(\frac{c}{a}\)
α × (6α) = \(\frac{8}{p}\)
6α² = \(\frac{8}{p}\)
6(\(\frac{2}{p}\))² = \(\frac{8}{p}\) ….[From (i)
⇒ \(\frac{6 \times 4}{p^2}\) = \(\frac{8}{p}\)
⇒ 8p = 24
∴ p = 3

Question 27.
From an external point, two tangents are drawn to a circle. Prove that the line joining the external point to the centre of the circle bisects the angle between the two tangents. 3
Answer:

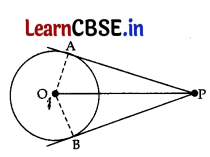
To Prove: ∠APO = ∠BPO
Construction: Join OA and OB.
Proof: AOAP and AOBP,
OP = OP…[Common
OA = OB …[Radii of same circle
PA = PB …[Tangents drawn from an external point are equal
ΔOAB ≅ ΔOBA …[By SSS ≅ rule
∠APO = ∠BPO
(Hence Proved) …[By CPCT

Section – D

Question 32.
(A) In a ΔPQR, N is a point on PR, such that QN⊥PR. If PN × NR = QN², prove that ∠PQR = 90°. 5
Or
(B) In the given figure, ΔABC and ΔDBC are on the same base BC.
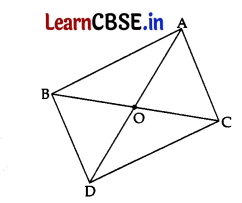
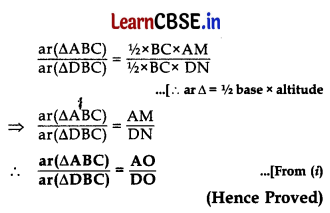
If AD intersects BC at O, prove that \(\frac{{ar}(\triangle \mathrm{ABC})}{{ar}(\triangle \mathrm{DBC})}=\frac{\mathrm{AO}}{\mathrm{DO}}\). 5

Answer:
(A)

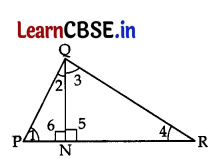
Proof: PN × NR = QN² …[Given
\(\frac{\mathrm{PN}}{\mathrm{QN}}\) = \(\frac{\mathrm{QN}}{\mathrm{NR}}\)
∠6 = ∠5 …[QN⊥PR, each 90°
ΔPNQ ~ ΔQNR …[By SAS similarity
∠1 = ∠3 ……(i) …[CPST
∠2 = ∠4 …(ii)
In ΔPQR, ∠1 + ∠PQR + ∠4 = 180° … [Angle-sum-Property of a Δ
⇒ ∠3 + ∠2 + ∠3 + ∠2 = 180° …[From (i) & (ii)
⇒ 2∠2 + 2∠3 = 180°
⇒ 2(∠2 + ∠3) = 180°
∴ ∠PQR = \(\frac{180^{\circ}}{2}\)
= 90° (Hence Proved)
Or
(B) Given: ΔABC and ΔDBC are two Δs on the same base BC and AD intersects BC at O.

To prove: \(\frac{{ar}(\triangle \mathrm{ABC})}{{ar}(\triangle \mathrm{DBC})}=\frac{\mathrm{AO}}{\mathrm{DO}}\)
Construction: Draw AM & DN⊥BC.
Proof: In ΔAMO and ΔDNO,
∠AMO = ∠DNO …[Each = 90°,
∠AOM = ∠DON …[Vertically opposite ∠s
∴ ΔAMO ~ ΔDNO …[AA corollary
\(\frac{\mathrm{AO}}{\mathrm{DO}}\) = \(\frac{\mathrm{AM}}{\mathrm{DN}}\) …(I) [In similar As corresponding
sides are proportional

Question 33.
A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in the figure. If the height of the cylinder is 10 cm and its base is of radius 3.5 cm, find the total surface area of the article. 5

Answer:

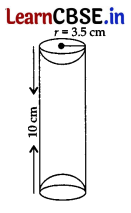
Here, h = 10 cm and r = 3.5 cm
∴ Total Surface area of the article
= C.S. area of cyl. + 2(C.S. area of hemisphere)
= 2πrh + 2(2πr²)
= 2πr(h + 2r)
= 2 × \(\frac{22}{7}\) × \(\frac{35}{10}\) (10 + 3.5 × 2)
= 22 × 17 = 374 cm²