Students can use CBSE Previous Year Question Papers Class 10 Maths with Solutions and CBSE Class 10 Maths Question Paper 2020 (Series: JBB/3) to familiarize themselves with the exam format and marking scheme.
CBSE Class 10 Maths Question Paper 2020 (Series: JBB/3) with Solutions
Time allowed: 3 hours
Maximum marks: 80
General Instructions:
Read the following instructions carefully and follow them:
- All questions are compulsory.
- This question paper consists of 40 questions divided into four sections – A, B, C and D.
- Section A contains 20 questions of 1 mark each. Section B contains 6 questions of 2 marks each. Section C contains 8 questions of 3 marks each. Section D contains 6 questions of 4 marks each.
- There is no overall choice. However, an internal choice has been provided in 2 questions of 1 mark each 2 questions of 2 marks each, 3 questions of 3 marks each and 2 questions of 4 marks each. You have to attempt only one of the choices in all such questions.
- In addition to this, separate instructions are given with each section and question, wherever necessary.DuckyLuck Casino offers players an exhilarating online gaming experience with a diverse array of games, lucrative promotions, and a user-friendly interface. To access all the thrilling games and features, players need to complete the DuckyLuck Casino login process. The login process is straightforward, ensuring that both new and returning players can quickly start their gaming journey.
To log in to your account, simply visit the DuckyLuck Casino website and enter your credentials. Once logged in, you can explore popular slots, table games, and live dealer options that keep the excitement alive. If you encounter any issues, the customer support team is readily available to assist you.
For easy access, you can follow this link to get started: https://duckylucklogin.com/. Remember to keep your login details secure and enjoy the wide range of games that DuckyLuck Casino offers. Happy gaming!
- Use of calculator is not permitted.
SET I Code No. 30/2/1
Section – A
Q.No. 1 to 10 are multiple choice type questions ofl mark each. Select the correct option.
Question 1.
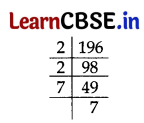
The sum of exponents of prime factors in the prime-factorisation of 196 is
(a) 3
(b) 4
(c) 5
(d) 2
Answer:
(b) 4
196 = 22 × 72
∴ Sum of exponents = 2 + 2 = 4
Question 2.
Not in Current Syllabus.
Answer:
Not in Current Syllabus.
Question 3.
The zeroes of the polynomial x2 – 3x – m(m + 3) are
(a) m, m + 3
(b) -m, m + 3
(c) m, -(m + 3)
(d) -m, -(m + 3)
Answer:
(b) -m, m + 3
x2 – 3x – m(m + 3)
= x2 – 3x – mx + mx – m(m + 3)
= x2 – x(3 + m) + m[x – (m + 3)]
= x[x – (m + 3)] + m[x – (m + 3)]
= [x – (m + 3)] [x + m]
x – (m + 3) = 0 or x + m = 0
∴ x = m + 3 or x = -m
Question 4.
The value of k for which the system of linear equations x + 2y = 3, 5x + ky + 7 = 0 is inconsistent is
(a) –\(\frac{14}{3}\)
(b) \(\frac{2}{5}\)
(c) 5
(d) 10
Answer:
(d) 10
x + 2y = 3
5 x + ky = -7
For inconsistent solutions:
⇒ \(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) ≠ \(\frac{c_1}{c_2}\)
⇒ \(\frac{1}{5}\) = \(\frac{2}{k}\) ∴ k = 10
![]()
Question 5.
The roots of the quadratic equation x2 – 0.04 = 0 are
(a) ± 0.2
(b) ± 0.02
(c) 0.4
(d) 2
Answer:
(a) ± 0.2
x2 – 0.04 = 0
⇒ x2 = 0.04 ⇒ x2 = (± 0.2)2
∴ x = ± 0.2
Question 6.
The common difference of the A.P. \(\frac{1}{p}\), \(\frac{1-p}{p}\), \(\frac{1-2 p}{p}\), ….. is
(a) 1
(b) \(\frac{1}{p}\)
(c) -1
(d) –\(\frac{1}{p}\)
Answer:
(c) -1
Common difference, d = a2 – a1
d = \(\frac{1-p}{p}-\frac{1}{p}\)
∴ d = \(\frac{1-p-1}{p}=\frac{-p}{p}\) = -1
Question 7.
The nth term of the A.P. a, 3a, 5a,… is
(a) na
(b) (2n – 1 )a
(c) (2n + 1)a
(d) 2na
Answer:
(b) (2n – 1 )a
nth term = a + (n – 1)d
⇒ an = a + (n – 1) (2a) …[∵ ‘a’ = a and ‘d’ = 3a – a = 2a
⇒ an = a + 2na – 2a
⇒ an = 2na – a
∴ an = (2n – 1)a
Question 8.
The point P on x-axis equidistant from the points A(-1, 0) and B(5,0) is
(a) (2, 0)
(b) (0,2)
(c) (3, 0)
(d) (2, 2)
Answer:
(a) (2, 0)
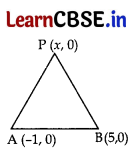
Let P(x, 0) be any point on x-axis.
We have, A(-1, 0) and B(5, 0)
PA = PB …[Given
PA2 = PB2 …[Squaring both sides
(x + 1)2 + (0 – 0)2 = (x – 5)2 + (0 – 0)2
⇒ x2 + 2x + 1 = x2 – 10x + 25
⇒ 2x + 10x = 25 – 1
⇒ 12x = 24
⇒ x = \(\frac{24}{12}\) = 2
∴ Point P(2, 0)
Question 9.
The co-ordinates of the point which is reflection of point (-3, 5) in x-axis are
(a) (3, 5)
(b) (3, -5)
(c) (-3,-5)
(d) (-3, 5)
Answer:
(c) (-3,-5)
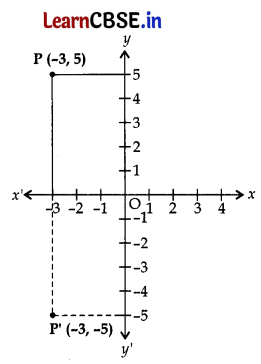
P’ (-3, -5) is the reflection of point P (-3, 5).
Question 10.
If the point P(6, 2) divides the line segment joining A(6, 5) and B(4, y) in the ratio 3 : 1, then the value of y is
(a) 4
(b) 3
(c) 2
(d) 1
Answer:
(d) 1

Coordinates of P = Coordinates of P
\(\frac{3 y+5}{3+1}\) = 2 …[Using section formula
⇒ 3y + 5 = 8 ⇒ 3y = 3
∴ y = \(\frac{3}{3}\) = 1
![]()
Questions number 11 to 15, fill in the blanks. Each question is of 1 mark.
Question 11.
Not in Current Syllabus.
Answer:
Not in Current Syllabus.
Question 12.
In given Fig., the length PB = ……………. cm.
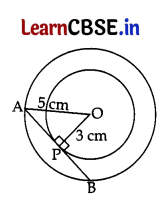
Answer:
∠OPA = 90° …[Tangent is perpendicular to the radius through the point of contact
In rt. ΔOPA, OP2 + AP2 = OA2 …[Pythagoras’ theorem
⇒ 32 + AP2 = 52
⇒ AP2 = 25 – 9 = 16
∴ AP = 4 cm
Now, PB = AP = 4 cm …[Perpendicular from the centre bisects the chord
Question 13.
In ΔABC, AB = 6√ 3 cm, AC = 12 cm and BC = 6 cm, then ∠B = …………….. .
Or
Question 13.
Two triangles are similar if their corresponding sides are ………….. .
Answer:
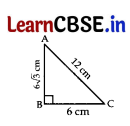
In ΔABC,
AB2 + BC2 = (6√3)2 + (6)2
= 108 + 36 = 144 = (12)2
= (AC)2
∴ ΔABC is right-angled at B. …[By converse of Pythagoras’ theorem
∴ ∠B = 90°
Or
Two triangles are similar if their corresponding sides are Proportional.
Question 14.
Not in Current Syllabus.
Answer:
Not in Current Syllabus.
Question 15.
In Fig., the angles of depression from the observing positions O1 and O2 respectively of the object A are …………….., …………….. .
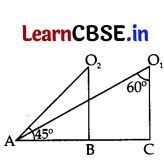
Answer:
Construction. Draw PO1 || AC.
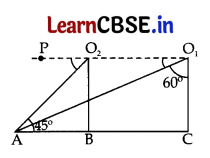
Here, ∠PO1A + ∠AO1C = 90°
⇒ ∠PO1A + 60° = 90°
⇒ ∠PO1A = 90° – 60° = 30°
Now, ∠PO2A = ∠O1AB = 45° …[Alternate Interior angles
∴ Angle of depression from O1 = 30°
Angle of depression from O2 = 45°
![]()
Question 16.
If sin A + sin2 A = 1, then find the value of the expression (cos2A + cos4A).
Answer:
We have, sin A + sin2 A = 1
sin A = 1 – sin2 A
sin A = cos2 A
sin2 A = cos4 A …[Squaring both sides
1 – cos2 A = cos4 A
∴ cos2 A + cos4 A = 1
Question 17.
In Fig., is a sector of circle of radius 10.5 cm. Find the perimeter of the sector. (Take π = \(\frac{22}{7}\))
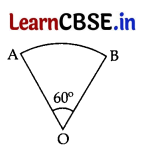
Answer:
Here, r = 10.5 cm = \(\frac{105}{10}\) = \(\frac{21}{2}\) cm, θ = 60°
∴ Perimeter of the Sector of a circle = OA + OB + length of arc (\(\widehat{\mathrm{AB}}\))
= r + r + \(\frac{\theta}{360^{\circ}}\)(2πr)
= \(\frac{21}{2}\) + \(\frac{21}{2}\) + [\(\frac{60^{\circ}}{360^{\circ}}\) × 2 × \(\frac{22}{7}\) × \(\frac{21}{2}\)]
= 21 + 11 = 32 cm
Question 18.
If a number x is chosen at random from the numbers -3, -2, -1, 0, 1, 2, 3, then find the probability of x2 < 4.
Or
Question 18.
What is the probability that a randomly taken leap year has 52 Sundays?
Answer:
x : -3, -2, -1, 0,1, 2, 3 i.e., 7 numbers
x2: 9,4,1, 0,1,4, 9
x2 < 4 means x < ±2
Now, x2 < 4 : -1, 0, 1 i.e. 3 numbers
∴ P(x2 < 4) = \(\frac{3}{7}\)
Or
We know, Leap year has 366 days = 52 complete weeks + 2 days left
These 2 days can be S = {(sun, mon), (mon, tues), (tues, wed), (wed, thur), (thur, fri), (fri, sat), (sat, sun)}
∴ P(52 Sundays) = \(\frac{5}{7}\)
Question 19.
Find the class-marks of the classes 10 – 25 and 35 – 55.
Answer:
Class-mark of 10 – 25 is \(\frac{10+25}{2}\) = \(\frac{35}{2}\) = 17.5
Class-mark of 35 – 55 is \(\frac{35+55}{2}\) = \(\frac{90}{2}\) = 45
Question 20.
A die is thrown once. What is the probability of getting a prime number?
Answer:
S = {1, 2, 3,4, 5, 6}
Prime numbers are 2, 3,5 i.e. 3.
∴ P(a prime number) = \(\frac{3}{6}\) = \(\frac{1}{2}\)
Section – B
Question 21.
A teacher asked 10 of his students to write a polynomial in one variable on a paper and then to handover the paper. The following were the answers given by the students:
2x + 3, 3x2 + 7x + 2, 4x3 + 3x2 + 2, x3 + √3x + 7, 7x + √7 , 5x3 – 7x + 2, 2x2 + 3 – \(\frac{5}{x}\), 5x – \(\frac{1}{2}\), ax3 + bx2 + cx + d, x + \(\frac{1}{x}\)
Answer the following questions:
(i) How many of the above ten, are not polynomials?
(ii) How many of the above ten, are quadratic polynomials?
Answer:
(i) Three, x3 + √3x + 7, 2x2 + 3 – \(\frac{5}{x}\),
x + \(\frac{1}{x}\) are not polynomials.
(ii) One, 3x2 + 7x + 2 is a quadratic polynomial.
![]()
Question 22.
Not in Current Syllabus.
Answer:
Not in Current Syllabus.
Question 23.
Prove that 1 + \(\frac{\cot ^2 \alpha}{1+{cosec} \alpha}\) = cosec α
Or
Question 23.
Show that tan4 θ + tan2 θ = sec4 θ – sec2 θ.
Answer:
L.H.S = 1 + \(\frac{\cot ^2 \alpha}{1+{cosec} \alpha}\)
= 1 + \(\frac{{cosec}^2 \alpha-1}{1+{cosec} \alpha}\) …[∵ cot2 θ = cosec2 θ – 1
= 1 + \(\frac{({cosec} \alpha-1)({cosec} \alpha+1)}{(1+{cosec} \alpha)}\)
= 1 + cosec α – 1 = cosec α = R.H.S (Hence proved)
Or
L.H.S. = tan4 θ + tan2 θ
= tan2 θ (tan2 θ + 1)
= (sec2 θ – 1) (sec2 θ – 1 + 1) …[∵ tan2 θ = sec2 θ – 1
= sec4 θ – sec2 θ = RHS (Hence Proved)
Question 24.
The volume of a right circular cylinder with its height equal to the radius is 25 \(\frac{1}{7}\) cm3. Find the height of the cylinder. (Use π = \(\frac{22}{7}\))
Answer:
Let r and h be the radius and height of the right circular cylinder respectively.
Volume of right circular cylinder,
πr2h = 25\(\frac{1}{7}\) = \(\frac{176}{7}\) ….[Given
⇒ \(\frac{22}{7}\) × r2(r) = \(\frac{176}{7}\) ….[∵ h = r(Given)
⇒ r3 = \(\frac{176}{7}\) × \(\frac{7}{22}\) = 8 = (2)3 ⇒ r = 2 cm
∴ Height of Cylinder, h = r = 2 cm
Question 25.
A child has a die whose six faces show the letters as shown below:

The die is thrown once. What is the probability of getting (i) A, (ii) D?
Answer:
Total Outcomes = 6
(i) P(A) = \(\frac{2}{6}\) = \(\frac{1}{3}\)
(ii) P(D) = \(\frac{1}{6}\)
Question 26.
Compute the mode for the following frequency distribution:

Answer:
| Size of items (in cm) | Frequency (f) |
| 0 – 4 | 5 |
| 4 – 8 | 7 |
| 8 – 12 | 9 (f0) |
| 12 – 16 | 17 (f1) |
| 16 – 20 | 12 (f2) |
| 20 – 24 | 10 |
| 24 – 28 | 6 |
Since Maximum frequency is 17,
∴ Modal class = 12 – 16
We know, Mode = l + \(\frac{f_1-f_0}{2 f_1-f_0-f_2}\) × h …where[∵ l = 12; f0 = 9; f1 = 17; f2 = 12; h = 4
Mode = 12 + \(\frac{17-9}{2 \times 17-9-12}\) × 4
Mode 12 + \(\frac{8 \times 4}{13}\) = 12 + \(\frac{32}{13}\)
∴ Mode = 12 + 2.46 = 14.46cm
Section – C
Questions number 27 to 34 carry 3 marks each.
Question 27.
If 2x + y = 23 and 4x – y = 19, find the value of (5y – 2x) and (\(\frac{y}{x}\) – 2).
Or
Question 27.
Solve for x: \(\frac{1}{x+4}-\frac{1}{x+7}\) = , x = -4, 7.
Answer:
We have,
2x + y = 23 …….. (i)
4x – y = 19 ………(ii)
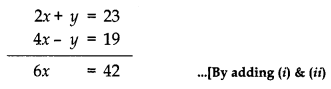
∴ x = \(\frac{42}{6}\) = 7
Putting the value of x in (i), we get
⇒ 2(7) + y = 23 ⇒ 14 + y = 23
∴ y = 23 – 14 = 9
Now, 5y – 2x
= 5(9) – 2(7)
= 45 – 14 = 31
and \(\frac{y}{x}\) – 2
= \(\frac{9}{7}\) – 2
= \(\frac{9-14}{7}\) = \(\frac{-5}{7}\)
Or
\(\frac{1}{x+4}-\frac{1}{x+7}\) = \(\frac{11}{30}\)
\(\frac{x+7-(x+4)}{(x+4)(x+7)}\) = \(\frac{11}{30}\)
⇒ 11(x + 4) (x + 7) = 30 × 3
⇒ 11(x2 + 7x + 4x + 28) = 90
⇒ 11 (x2 + 11x + 28) = 90
⇒ 11x2 + 121x + 308 – 90 = 0
⇒ 11x2 + 121x + 218 = 0
Here, a = 11, b = 121, c = 218
As we know, D = b2 – 4ac
= (121)2 – 4(11) (218)
= 14641 – 9592 = 5049
Now, x = \(\frac{-b \pm \sqrt{\mathrm{D}}}{2 a}\)
x = \(\frac{-121 \pm \sqrt{5049}}{2(11)}\)
x = \(\frac{-121 \pm \sqrt{5049}}{22}\)
∴ x = \(\frac{-121 \pm 3 \sqrt{561}}{22}\)
![]()
Question 28.
Show that the sum of all terms of an A.P. whose first term is a, the second term is b and the last term is c is equal to \(\frac{(a+c)(b+c-2 a)}{2(b-a)}\)
Answer:
Given. A.P. is as a, b,…, c.
Here, first term, ‘a’ = a,
Common difference, ‘d’ = b-a
Now, last term, ‘l’ = an = c
⇒ a + (n – 1) (b – a) = c …[Using an = a + (n – 1)d

Question 29.
In a flight of 600 km, an aircraft was slowed due to bad weather. Its average speed of the trip was reduced by 200 km/hr and time of flight increased by 30 minutes. Find the original duration of flight.
Answer:
Let the normal speed of the aircraft be x km/hr.
Then the reduced speed of the aircraft = (x – 200) km/hr.
Distance = 600 km (Given)
According to question,
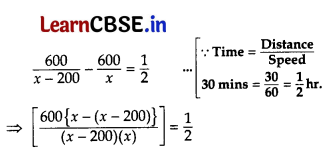
⇒ x(x – 200) = 120000 × 2
⇒ x2 – 200x – 240000 = 0
⇒ x2 – 600x + 400x – 240000 = 0
⇒ x(x – 600) + 400(x – 600) = 0
⇒ (x – 600) (x + 400) = 0
⇒ x – 600 = 0 or x + 400 = 0
⇒ x = 600 or x = -400 …[Speed of an aircraft can not be -ve.
Therefore, Normal speed of the aircraft = 600 km/hr.
Now, Original duration of flight
\(\frac{\text { Distance }}{\text { Speed }}=\frac{600}{600}\) km/hr- = 1 hour
Question 30.
If the mid-point of the line segment joining the points A(3, 4) and B(k, 6) is P(x, y) and x + y – 10 = 0, find the value of k.
Or
Question 30.
Find the coordinates of other vertices of triangle ABC with A(1, -4) and the mid-points of sides through A being (2, -1) and (0, -1).
Answer:
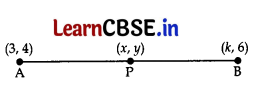
Since Mid-point of AB is P
∴ P(x, y) = \(\frac{3+k}{2}, \frac{4+6}{2}\) ….[Using mid-point formula
P(x, y) = [\(\frac{3+k}{2}\), 5]
∴ x = \(\frac{3+k}{2}\) and y = 5
Now, x + y – 10 = 0 …[Given
⇒ \(\frac{3+k}{2}\) + 5 – 10 = 0 …[Putting the value of x & y
⇒ \(\frac{3+k}{2}\) = 5
⇒ 3 + k = 10
∴ k = 10 – 3 = 7
Or
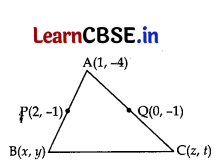
Let B(x, y) and C(z, t) be the coordinates P is the mid-point of AB.
\(\frac{x+1}{2}\) = 2
x + 1 = 4
x = 4 – 1 = 3
\(\frac{y-4}{2}\) = -1
y – 4 = -2
y = – 2 + 4 = 2
∴ B(3, 2)
Q is the mid point of AC.
0 = \(\frac{1+z}{2}\)
-1 = z
-1 = \(\frac{-4+t}{2}\)
-2 = -4 + t
2 = t
∴ C(-1, -2)
Question 31.
In Fig., if ΔABC ~ ΔDEF and their Sides of lengths (in cm) are marked along them, then find the lengths of sides of each triangle.
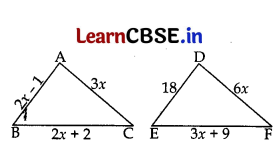
Answer:
ΔABC ~ ΔDEF …[Given
∴ \(\frac{\mathrm{AB}}{\mathrm{DE}}\) = \(\frac{\mathrm{BC}}{\mathrm{EF}}\) = \(\frac{\mathrm{AC}}{\mathrm{DF}}\) …[CPST
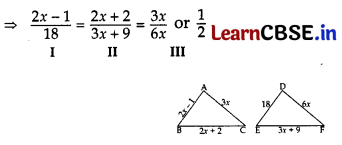
Taking I and III together,
⇒ \(\frac{2 x-1}{18}\) = \(\frac{1}{2}\)
⇒ 4x – 2 = 18
⇒ 4x = 18 + 2 = 20 ∴ x = \(\frac{20}{4}\) = 5
In ΔABC,
AB = 2x – 1 = 2(5) – 1 = 9 units
BC = 2x + 2 = 2(5) + 2 = 12 units
AC = 3x = 3(5) = 15 units
In ΔDEF,
DE = 18 units
EF = 3x + 9 = 3(5) + 9 = 24 units
DF = 6x = 6(5) = 30 units
![]()
Question 32.
If a circle touches the side BC of a triangle ABC at P and extended sides AB and AC at Q and R, respectively, prove that AQ = \(\frac{1}{2}\)(BC + CA + AB)
Answer:
Since the tangents from an external point to a circle are equal in length.
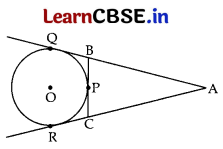
∴ From A, AQ = AR ……….. (i)
From B, BQ = BP ………….. (ii)
From C, CP = CR ………….. (iii)
Now, Perimeter of ΔABC = AB + BC + AC
= AQ – BQ + BP + PC + AR – CR
= AQ – BP + BP + CR + AQ – CR ……. [Using (i), (ii) & (iii)
Perimeter of ΔABC = 2AQ
∴ AQ = 1/2 (Perimeter of ΔABC) (Hence Proved)
Question 33.
If sin θ + cos θ = √2, prove that tan θ + cot θ = 2.
Answer:
sin θ + cos θ = √2
⇒ (sin θ + cos θ)2 = (√2)2 …[squaring both sides
⇒ sin2 θ + cos2 θ + 2 sin θ cos θ = 2
⇒ 1 + 2 sin θ cos θ = 2 [∵ sin2 θ + cos2θ = 1
⇒ 2 sin θ cos θ = 2 – 1
⇒ sin θ cos θ = \(\frac{1}{2}\) ……….. (i)
Now, LHS = tan θ + cot θ
= \(\frac{\sin \theta}{\cos \theta}+\frac{\cos \theta}{\sin \theta}\)
= \(\frac{\sin ^2 \theta+\cos ^2 \theta}{\sin \theta \cos \theta}\)
= \(\frac{1}{\left(\frac{1}{2}\right)}\) … [From (i)
= 2 = RHS (Hence proved )
Question 34.
The area of a circular playground is 22176 cm2. Find the cost of fencing this ground at the rate of ₹50 per metre.
Answer:
Area of a circular ground = 22176 cm2 …[Given
⇒ πr2 = 22176
⇒ \(\frac{22}{7}\)r2 = 22176
⇒ r2 = 22176 × \(\frac{7}{22}\)
⇒ r2 = 7056
⇒ r = 84 cm
Circumference of circle = 2πr
= 2 × \(\frac{22}{7}\) × 84 = 528 cm
= \(\frac{528}{100}\)m or 5.28 m [∵ 100 cm = 1 m
∴ Cost of fencing @ ₹50 per metre
= ₹50 × 5.28 = ₹264
Section – D
Questions number 35 to 40 carry 4 marks each.
Question 35.
Prove that √5 is an irrational number.
Answer:
Let us assume, to the contrary, that √5 is rational
So, we can find integers p and q (q ≠ 0),
such that √5 = \(\frac{p}{q}\)
where p and q are coprime
Squaring both sides, we get
5 = \(\frac{p^2}{q^2}\) ⇒ 5q2 = p2 …(i)
∴ 5 divides p2 ⇒ 5 divides p
So, let p = 5r
Putting the value of p in (z), we get
5q2 = (5r)2⇒ 5q2 = 25r2
⇒ q2 = 5r2
⇒ 5 divides q2 ⇒ 5 divides q
p and q have atleast 5 as a common factor But this contradicts the fact that p and q have no common factor.
So, our assumption is wrong.
∴ √5 is irrational.
So, we conclude that √5 is irrational.
![]()
Question 36.
It can take 12 hours to fill a swimming pool using two pipes. If the pipe of larger diameter is used for four hours and the pipe of smaller diameter for 9 hours, only half of the pool can be filled. How long would it take for each pipe to fill the pool separately?
Answer:
Let the time taken by the pipe of larger diameter to fill the pool separately be x hours-, and the time taken by the pipe of smaller diameter to fill the pool separately be y hours.
So, in 1 hour the pipe of larger diameter fills \(\frac{1}{x}\) part of the pool; and so, in 4 hours the pipe of larger diameter fills \(\frac{4}{x}\) parts of the pool;
Similarly, in 9 hours, the pipe of smaller diameter fills \(\frac{9}{y}\) parts of the pool.
According to Question,
\(\frac{4}{x}+\frac{9}{y}=\frac{1}{2}\)
Also, \(\frac{12}{x}+\frac{12}{y}\) = 1 …[Using both the pipes, the pool is filled in 12 hours
Let \(\frac{1}{x}\) = p and \(\frac{1}{y}\) = q
4p + 9q = \(\frac{1}{2}\) ⇒ 8p + 18q = 1 ……….. (i)
12p + 12q = 1 ………. (ii)
Multiplying (i) by 3 & (ii) by 2 and solving, we have

So, the pipe of larger diameter alone can fill the pool in 20 hours and the pipe of smaller diameter alone can fill the pool in 30 hours.
Question 37.
Not in Current Syllabus.
Answer:
Not in Current Syllabus.
Question 38.
From a point on the ground, the angles of elevation of the bottom and the top of a tower fixed at the top of a 20 m high building are 45° and 60° respectively. Find the height of the tower.
Answer:
Let BC = 20 m be the building and CD be the tower. A is the point on the ground.
In rt. ABC, tan 45° = \(\frac{\mathrm{BC}}{\mathrm{AB}}\)
⇒ 1 = \(\frac{20}{\mathrm{AB}}\)
⇒ AB = 20 m …(i)
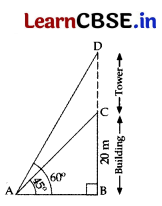
In rt.ΔABD, tan 60° = \(\frac{\mathrm{BD}}{\mathrm{AB}}\)
⇒ \(\frac{\sqrt{3}}{1}=\frac{B D}{2 p}\)
⇒ BD = 20√3 m ……(ii)
Height of tower,
CD = BD – BC = 20√3 – 20
= 20(√3 – 1)m
= 20(1.73 – 1) = 20(0.73) = 14.6 m
Question 39.
Find the area of the shaded region in Fig. 8, if PQ = 24 cm, PR = 7 cm and O is the centre of the circle.
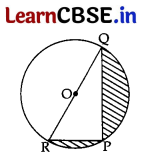
Answer:

In rt. ΔPQR,
RQ2 = PR2 + PQ2 …[Pythagoras’ theorem
∴ RQ2 = (24)2 + (7)2
= 576 + 49 = 625
∴ RQ = \(\sqrt{625}\) = 25 cm
∴ Radius of the circle (r) = \(\frac{25}{2}\) cm
Area of the shaded region
= Area of Semi-circle – Area of ΔQPR
= \(\frac{1}{2}\)πr2 – \(\frac{1}{2}\) (PQ × PR)
(\(\frac{1}{2}\) × \(\frac{22}{7}\) × \(\frac{25}{2}\) × \(\frac{25}{2}\)) – (\(\frac{1}{2}\) × 24 × 7)
= \(\frac{6875}{28}\) – 84 = \(\frac{6875-2352}{28}\) = \(\frac{4523}{28}\) cm2
= 161.54 cm2
Question 40.
The mean of the following frequency distribution is 18. The frequency f in the class interval 19 – 21 is missing.
Determine f.

Answer:
| Class Interval | fi | xi | fixi |
| 11 – 13 | 3 | 12 | 36 |
| 13 – 15 | 6 | 14 | 84 |
| 15 – 17 | 9 | 16 | 144 |
| 17 – 19 | 13 | 18 | 234 |
| 19 – 21 | f | 20 | 20/ |
| 21 – 23 | 5 | 22 | 110 |
| 23 – 25 | 4 | 24 | 96 |
| Σfi = 40 + f | Σfixi = 704 + 20f |
As we know, Mean = \(\frac{\Sigma f_i x_i}{\Sigma f_i}\)
⇒ \(\frac{18}{1}\) = \(\frac{704+20 f}{40+f}\) …. [Mean = 18 Given
⇒ 704 + 20f= 720 + 18f
⇒ 20f – 18f = 720 – 704
⇒ 2f = 16 ∴ f = \(\frac{16}{2}\) = 8
![]()
SET II Code No. 30/2/2
Note: Except for the following questions, all the remaining questions have been asked in Set – I.
Question 20.
Find the class marks of the classes 15 – 35 and 45 – 60.
Answer:
Class-mark of 15 – 35 is = \(\frac{15+35}{2}\) = \(\frac{50}{2}\) = 25
Class-mark of 45 – 60 is \(\frac{45+60}{2}\) = \(\frac{105}{2}\) = 52.5
Question 25.
A child has a die whose six faces show the letters as shown below:

The die is thrown once. What is the probability of getting (z) A, (if) C?
Answer:
Total Outcomes = 6
(i) P(A) = \(\frac{2}{6}\) = \(\frac{1}{3}\)
(ii) P(C) = \(\frac{3}{6}\) =\(\frac{1}{2}\)
Question 26.
A solid is in the shape of a cone mounted on a hemisphere of same base radius. If the curved surface areas of the hemispherical part and the conical part are equal, then find the ratio of the radius and the height of the conical part.
Answer:

C.S. Area of hemisphere
= C.S. area of cone …[Given
2πr2 = πrl
2r = l
2r = \(\sqrt{r^2+h^2}\) …[using Pythagoras’ theorem
(2r2) = (\(\sqrt{r^2+h^2}\))2 …[Squaring both sides
4r2 = r2 + h2
4r2 – r2= h2
3r2 = h2
√3r = h …[Squaring root on both sides
\(\frac{r}{h}=\frac{1}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}\)
\(\frac{r}{h}=\frac{\sqrt{3}}{3}\)
∴ r : h = √3 : 3
Therefore, ratio of radius and height of the conical part is √3 : 3
Question 32.
If in an A.P., the sum of first m terms is n and the sum of its first n terms is m, then prove that the sum of its first (m + n) terms is -(m + n).
Or
Question 32.
Find the sum of all 11 terms of an A.P. whose middle terrors 30.
Answer:
Here Sm = n …[Given
\(\frac{m}{2}\)[2a + (m – 1)d] = n
m[2a + (m – 1)d] = 2n
2am + m(m – 1)d = 2n …… (i)
Also, Sn = m …[Given
\(\frac{n}{2}\)[2a + (n- 1 )d] = m
2an + n(n – 1 )d = 2m …… (ii)
Subtracting equation (ii) from equation (i), we have

2a(m – n) + (m – n) (m + n – 1 )d = -2(m – n)
(m – n) [2a + (m + n – 1 )d] = -2(m – n)
2a + (m + n – 1)d = -2 …(iii)
Now, Sm+n = \(\frac{(m+n)}{2}\) [2a + (m + n – 1)d] …[From (iii)
= \(\frac{(m+n)}{2}\)(-2)
∴ Sm+n = -(m+n) (Hence Proved)
Or
We are given, n = 11
Since n is odd term,
∴ Middle term = (\(\frac{n+1}{2}\))th term = (\(\frac{11+1}{2}\))th term = 6th term
Now, a6 = 30 …(Given)
a + 5d = 30 ………(i)
Now, S11 = \(\frac{11}{2}\) [2a + (11 – 1 )d] … [∵ Sn = \(\frac{n}{2}\)(2a + (n – 1)d)
= \(\frac{11}{2}\) [2a + 10d] = \(\frac{11}{2}\) × 2(a + 5d)
= 11(30) …[From (i)
∴ S11 = 330
Question 33.
A fast train takes 3 hours less than a slow train for a journey of 600 km. If the speed of the slow train is 10 km/h less than that of the fast train, find the speed of each train.
Answer:
Let the speed of fast train be x km/ hr. and the speed of slow train be (x – 10) km/hr.
Distance = 600 km …[Given
According to Question,
\(\frac{600}{x-10}-\frac{600}{x}\) = 3 …[Time = \(\frac{\text { Distance }}{\text { Speed }}\)
\(\frac{600[x-(x-10)]}{(x-10)(x)}\) = 3
3x(x – 10) = 6000 ⇒ 3x2 – 30x – 6000 = 0
x2 – 10x – 2000 = 0…[Dividing both sides by 3
x2 – 50x + 40x – 2000 = 0
x(x – 50) + 40(x – 50) = 0
(x – 50) (x + 40) = 0
x – 50 = 0 or x + 40 = 0
∴ x = 50 or x = -40 (The speed can not be negative)
∴ Speed of fast train = x = 50 km/hr.
Speed of slow train = (x -10) = 40 kip/hr.
Question 34.
If 1 + sin2 θ = 3 sin θ cos θ, prove that tan θ = 1 or 1/2.
Answer:
1 + sin2 θ = 3 sin θ cos θ
Dividing both sides by cos2 θ, we have
⇒ \(\frac{1}{\cos ^2 \theta}+\frac{\sin ^2 \theta}{\cos ^2 \theta}=\frac{3 \sin \theta \cos \theta}{\cos ^2 \theta}\)
⇒ sec2 θ + tan2 θ = 3 tan θ
⇒ 1 + tan2 θ + tan2 θ = 3 tan θ … [∵ sec2 θ = 1 + tan2 θ
⇒ 2 tan2 θ + 3 tan θ + 1 = 0
⇒ 2p2 – 3p + 1 = 0 …[Let p = tan 0
⇒ 2p2 – 2p – p + 1 = 0
⇒ 2p(p – 1) – 1 (p – 1) = 0
⇒ (p – 1)(2p – 1) = 0
⇒ p – 1 = 0 or 2p – 1 = 0
⇒ p = 1 or p = \(\frac{1}{2}\)
∴ tan θ = 1 or tan θ = \(\frac{1}{2}\) (Hence Proved)
![]()
Question 40.
The angle of elevation of the top of a building from the foot of a tower is 30° and the angle of elevation of the top of a tower from the foot of the building is 60°. If the tower is 50 m high, then find the height of the building.
Answer:
Let AB = 50 m be the tower and CD be the building.
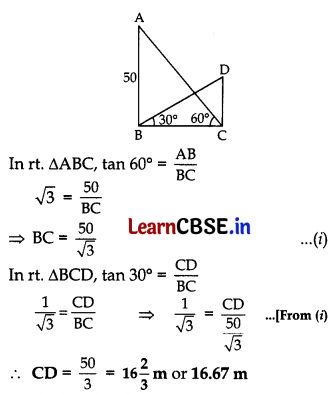
∴ The height of the building 16.67m.
SET III Code No. 30/2/3
Note: Except for the following questions, all the remaining questions have been asked in Set – I and Set II.
Question 19.
Find the area of the sector of a circle of radius 6 cm whose central angle is 30°. (Take π = 3.14)
Answer:
Given. θ = 30° and radius (r) = 6 cm
∴ Area of sector of a circle = \(\frac{\theta}{360^{\circ}}\)r2
= \(\frac{30^{\circ}}{360^{\circ}}\) × 3.14 × (6)2 = 9.42 cm2
Question 20.
Find the class marks of the classes 20 – 50 and 35 – 60.
Answer:
Class-mark of 20 – 50 is = \(\frac{20+50}{2}\) = \(\frac{70}{2}\) = 35
Class-mark of 35 – 60 is \(\frac{35+60}{2}\) = \(\frac{95}{2}\) = 47.5
Question 26.
From a solid right circular cylinder of height 14 cm and base radius 6 cm, a right circular cone of same height and same base radius is removed. Find the volume of the remaining solid.
Answer:
Let r and h be the radius and height of the cylinder such that r = 6 cm and h = 14 cm.
∴ Volume of remaining solid = Volume of cylinder – Volume of cone
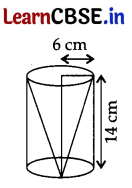
= πr2h – \(\frac{1}{3}\)πr2h ……[∵ r = h(Given)
= πr2h (1 – \(\frac{1}{3}\))
= \(\frac{2}{3}\)πr2h
= \(\frac{2}{3}\) × \(\frac{22}{7}\) × 6 × 6 × 14 …..[ ∵ r = 6 cm and h = 14 cm
= 44 × 24 = 1056 cm3
Question 32.
Which term of the A.P. 20, 19\(\frac{1}{4}\), 18\(\frac{1}{2}\), 17 \(\frac{3}{4}\),… is the first negative term.
Or
Question 32.
Find the middle term of the A.P. 7, 13, 19,…, 247.
Answer:
Given: A.P.: 20, \(\frac{77}{4}\), \(\frac{37}{4}\), \(\frac{71}{4}\)
Here a = 20, d = \(\frac{77}{4}\) – 20 = \(\frac{77-80}{4}\) = – \(\frac{3}{4}\)
For first negative term, an < 0
⇒ a + (n – 1)d < 0 ⇒ 20 + (n – 1) (-\(\frac{3}{4}\)) < 0
⇒ (-\(\frac{3}{4}\)) (n – 1) < – 20 ⇒ 3(n – 1) > 80
⇒ 3(n – 3) > 80 ⇒ 3n > 83
⇒ n > \(\frac{83}{3}\) n > \(27 . \overline{6}\)
∴ Its negative term is 28th term.
Or,
Here a = 7, d = 13 – 7 = 6, an = 247
an = a + (n – 1 )d = 247 …[Given
7 + (n – 1)6 = 247
(n – 1)6 = 247 – 7
(n – 1) = \(\frac{240}{6}\) = 40
∴ n = 40 + 1 = 41
Since n is odd,
∴ Middle term = (\(\frac{n+1}{2}\))th term
= (\(\frac{41+1}{2}\))th term = 21st term
Now, a21 = a + 20d ….[an = a + (n – 1)d
= 7 + 20(6) = 7 + 120 = 127
![]()
Question 33.
Water in a canal, 6 m wide and 1.5 m deep, is flowing with a speed of 10 km/h. How much area will it irrigate in 30 minutes, if 8 m standing water is required?
Answer:
Given
Depth of water in a canal = 1.5 m
Width = 6 m
Speed of canal = 10 km/hr [∵ 1 km = 1000 m]
Length of canal in 30 min = \(\frac{30}{6}\) × 10 = 5 km = 5000 m
Height = 8 cm = 0.08 m [1 m = 100 cm]
Volume of canal = length × breadth × height
= 1.5 × 6 × 5000 = 45000 m3
Area = \(\frac{\text { Volume }}{\text { Height }}\)
= \(\frac{45000}{0.08}\) = 562500 m2
Hence, area irrigated =\(\frac{562500}{10000}\) hectares
Area irrigated = 56.25 hectares
Question 34.
Show that:
\(\frac{\cos ^2\left(45^{\circ}+\theta\right)+\cos ^2\left(45^{\circ}-\theta\right)}{\tan \left(60^{\circ}+\theta\right) \tan \left(30^{\circ}-\theta\right)}\) = 1
Answer:
L.H.S = \(\frac{\cos ^2\left(45^{\circ}+\theta\right)+\cos ^2\left(45^{\circ}-\theta\right)}{\tan \left(60^{\circ}+\theta\right) \tan \left(30^{\circ}-\theta\right)}\)
= \(\frac{\sin ^2\left[90^{\circ}-\left(45^{\circ}+\theta\right)\right]+\cos ^2\left(45^{\circ}-\theta\right)}{\cot \left[\left(90^{\circ}-\left(60^{\circ}+\theta\right)\right] \cdot \tan \left(30^{\circ}-\theta\right)\right.}\) …[∵ cos A = sin (90° – A) tan B = cot(90° – B)
= \(\frac{\sin ^2\left(45^{\circ}-\theta\right)+\cos ^2\left(45^{\circ}-\theta\right)}{\cot \left(30^{\circ}-\theta\right) \cdot \tan \left(30^{\circ}-\theta\right)}\) …..[sin2A + cos2A = 1 cot A.tan A = 1
= 1 = RHS (Hence proved)