Students can use CBSE Previous Year Question Papers Class 10 Maths with Solutions and CBSE Class 10 Maths Question Paper 2020 (Series: JBB/1) to familiarize themselves with the exam format and marking scheme.
CBSE Class 10 Maths Question Paper 2020 (Series: JBB/1) with Solutions
Time allowed: 3 hours
Maximum marks: 80
General Instructions:
Read the following instructions carefully and follow them:
- All questions are compulsory.
- This question paper consists of 40 questions divided into four sections – A, B, C and D.
- Section A contains 20 questions ofl mark each. Section B contains 6 questions of 2 marks each. Section C contains 8 questions of 3 marks each. Section D contains 6 questions of 4 marks each.
- There is no overall choice. Hmvever, an internal choice has been provided in 2 questions ofl mark each 2 questions of 2 marks each, 3 questions of 3 marks each and 2 questions of 4 marks each. You have to attempt only one of the choices in all such questions.
- In addition to this, separate instructions are given with each section and question, wherever necessary.
- Use of calculator is not permitted.
SET Code No. 30/1/1
Section – A
Q.No. 1 to 10 are multiple choice type questions of 1 mark each. Select the correct option.
Question 1.
If one of the zeroes of the quadratic polynomial x2 + 3x + k is 2, then the value of k is
(a) 10
(b) -10
(c) -7
(d) -2
Answer:
(b) -10
Let P(x) = x2 + 3x + k
⇒ P(2) = (2)2 + 3(2) + k
⇒ 0 = 4 + 6 + k ⇒ 10 + k = 0 …. [∵ ‘2’ is a zero of P(x)
∴ k = -10
Question 2.
The total number of factors of a prime number is
(a) 1
(b) 0
(c) 2
(d) 3
Answer:
(c) 2
The total number of factors of a prime number are 2 i.e., ‘1’ and the ‘number itself’.
Question 3.
The quadratic polynomial, the sum of whose zeroes is -5 and their product is 6, is
(a) x2 + 5x + 6
(b) x2 – 5x + 6
(c) x2 – 5x – 6
(d) -x2 + 5x + 6
Answer:
(a) x2 + 5x + 6
As we know, x2 – Sx + P ……where [S & P are the sum and product of zeroes respectively
= x2 – (-5)x + 6 …[Given: S = -5, P = 6
= x2 + 5x + 6
![]()
Question 4.
The value of k for which the system of equations x + y – 4 = 0 and 2x + ky = 3, has no solution, is
(a) -2
(b) ≠2
(c) 3
(d) 2
Answer:
(d) 2
We have, x + y = 4 and 2x + ky = 3
For no solution: \(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) ≠ \(\frac{c_1}{c_2}\)
\(\frac{1}{2}\) = \(\frac{1}{k}\) ≠ \(\frac{4}{3}\)
\(\frac{1}{2}\) = \(\frac{1}{k}\) ∴ k = 2
Question 5.
The HCF and LCM of 12, 21,15 respectively are
(a) 3, 140
(b) 12, 420
(c) 3, 420
(d) 420, 3
Answer:
(c) 3, 420
Here, 12 = 2 × 2 × 3
21 = 3 × 7
15 = 3 × 5
∴ HCF = 3
∴ LCM = 22 × 3 × 5 × 7 = 420
Question 6.
The value of x for which 2x, (x + 10) and (3x + 2) are the three consecutive terms of an AP, is
(a) 6
(b) -6
(c) 18
(d) -18
Answer:
(a) 6
Since 2x, (x + 10), (3x + 2) are in A.P.
⇒ 2(x + 10) = 2x + 3x + 2 ….[If a, b and c are in A.P. then b – a = c – b or 2b = c + a
⇒ 2x + 20 = 5x + 2
⇒ 20 – 2 = 5x – 2x
⇒ 18 = 3x ∴ x = \(\frac{18}{3}\) = 6
Question 7.
The first term of an AP is p and the common difference is q, then its 10th term is
(a) q + 9p
(b) p – 9q
(c) p + 9q
(d) 2p + 9q
Answer:
(c) p + 9q
a10 = a + (10 – 1 )d
a10 = a + 9 d
∴ a10 = P + 9q …[Given: ‘a’ = p & ‘d’ = q
Question 8.
The distance between the points (a cos θ + b sin θ,0) and (0, a sin θ – b cos θ) is
(a) a2 + b2
(b) a2 – b2
(c) \(\sqrt{a^2+b^2}\)
(d) \(\sqrt{a^2-b^2}\)
Answer:
(c) \(\sqrt{a^2+b^2}\)
Let A (a cos θ + b sin θ, 0) and B(0, a sin θ – b cos θ).

= \(\sqrt{a^2(1)+b^2(1)}\) ..[∵ sin2θ + cos2θ = 1
∴ AB = \(\sqrt[1]{a^2+b^2}\)
Question 9.
If the point P(k, 0) divides the line segment joining the points A(2, -2) and B(-7,4) in the ratio 1 : 2, then the value of k is
(a) 1
(b) 2
(c) -2
(d) -1
Answer:
(d) -1
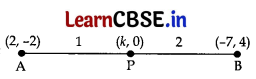
Here AP : PB = 1 : 2 …[Given
k = \(\frac{1(-7)+2(2)}{1+2}\) …[Using section formula
∴ k = \(\frac{-7+4}{3}\) = \(\frac{-3}{3}\) = -1
Question 10.
Not in Current Syllabus.
Answer:
Not in Current Syllabus.
Questions number 11 to 15, fill in the blanks. Each question is of 1 mark.
![]()
Question 11.
In Fig., ΔABC is circumscribing a circle, the length of BC is …………….. cm.
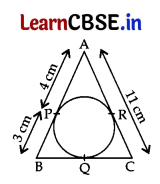
Answer:
AR = AP = 4 cm …[Tangents drawn from an external point are equal
∴ CR = AC – AR = 11 – 4 = 7 cm
∴ BQ = BP = 3 cm
∴ QC = CR = 7 cm …[Tangents drawn from an external point are equal
Here, BC = BQ + QC = 3 + 7
∴ BC = 10 cm
Question 12.
Not in Current Syllabus.
Answer:
Not in Current Syllabus.
Question 13.
Not in Current Syllabus.
Answer:
Not in Current Syllabus.
Question 14.
Not in Current Syllabus.
Answer:
Not in Current Syllabus.
Question 15.
The value of (sin2 θ + \(\frac{1}{1+\tan ^2 \theta}\)) = …………… .
Or
Question 15.
The value of (1 + tan2 θ) (1 – sin θ) (1 + sin θ) = …………… .
Answer:
sin2 θ + \(\frac{1}{1+\tan ^2 \theta}\)
= sin2 θ + \(\frac{1}{\sec ^2 \theta}\) ..[∵ 1 + tan2 θ = sec2 θ
= sin2 θ + cos2 θ …[∵ \(\frac{1}{\sec ^2 \theta}\) = cos2 θ
= 1
Or
(1 + tan2 θ) (1 – sin θ) (1 + sin θ)
= (1 + \(\frac{\sin ^2 \theta}{\cos ^2 \theta}\)) (1 – sin2θ)
= (\(\frac{\cos ^2 \theta+\sin ^2 \theta}{\cos ^2 \theta}\)) cos2 θ = 1 …[∵ cos2 θ + sin2 θ = 1
Questions number 16 to 20 are short answer type questions ofl mark each.
Question 16.
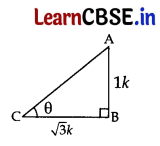
The ratio of the length of a vertical rod and the length of its shadow is 1 : √3 Find the angle of elevation of the sun at that moment?
Answer:
Let AB be the vertical rod and BC the length of its shadow.
Let AB = 1k and BC = √3k
tan θ = \(\frac{\mathrm{AB}}{\mathrm{BC}}\)
tan θ = \(\frac{1 k}{\sqrt{3} k}=\frac{1}{\sqrt{3}}\) = tan 30° [∵ tan 30° = \(\frac{1}{\sqrt{3}}\)
∴ θ(Angle of elevation of the sun) = 30°
Question 17.
Two cones have their heights in the ratio 1 : 3 and radii in the ratio 3 : 1. What is the ratio of their volumes?
Answer:
Let the height of 1st and 2nd cone be 1p and 3p respectively. Let the radius of 1st and 2nd cone be 3q and 1 q respectively.
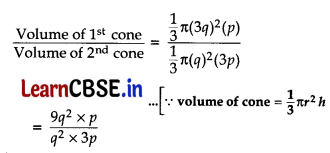
∴ Required Ratio = 3 : 1
![]()
Question 18.
A letter of English alphabet is chosen at random. What is the probability that the chosen letter is a consonant.
Answer:
Total alphabets = 26
Number of consonants = 26 – 5 = 21 …[Except vowels i.e. a, e, i, o, u
∴ P(a consonant) = \(\frac{21}{26}\)
Question 19.
A die is thrown once. What is the probability of getting a number less than 3?
Or
Question 19.
If the probability of winning a game is 0.07, what is the probability of losing it?
Answer:
Total Outcomes, S = {1, 2, 3, 4, 5, 6} i.e., six Numbers less than 3 are 1 and 2, i.e., two.
∴ P(a number less than 3) = \(\frac{2}{6}\) = \(\frac{1}{3}\)
Or
Since P(winning the game) = 0.07 …[Given
∴ P(losing the game) = 1 – P(winning the game) …[∵ P(E) + P(\(\overline{\mathbf{E}}\)) = 1
= 1 – 0.07 = 0.93
Question 20.
If the mean of the first n natural numbers is 15, then find n.
Answer:
Sum of first n natural nos. is \(\frac{n(n+1)}{2}\)
Mean (\(\bar{X}\)) = \(\frac{\Sigma x_i}{n}\)
⇒ 15 = \(\frac{\frac{n(n+1)}{2}}{n}\) ⇒ 15 = \(\frac{n+1}{2}\)
⇒ n + 1 = 30
∴ n = 30 – 1 :: 29
Section – B
Questions number 21 to 26 carry 2 marks each.
Question 21.
Show that (a – b)2, (a2 + b2) and (a + b)2 are in AP.
Answer:
Let a1 = (a – b)2; a2 = (a2 + b2); a3 = (a + b)2
a2 – a1 = a2 + b2 – (a – b)2
= a2 + b2 – (a2 + b2 – 2ab) = 2ab ……(i)
a3 – a2 = (a + b)2 – (a2 + b2)
= a2 + b2 + 2ab – a2 – b2 = 2ab ……(ii)
From (i) and (ii), a2 – a1 = a3 – a2 = 2ab
Therefore, (a – b)2, (a2 + b2) and (a + b)2 are in A.P.
Question 22.
In Fig, DE || AC and DC || AP. Prove that \(\frac{\mathrm{BE}}{\mathrm{EC}}\) = \(\frac{\mathrm{BC}}{\mathrm{CP}}\).

Or
Question 22.
In Fig., two tangents TP and TQ are drawn to a circle with centre O from an external point T. Prove that ∠PTQ =2∠OPQ
Answer:
Proof: In ΔABC, DE || AC …Given
∴ \(\frac{\mathrm{BD}}{\mathrm{DA}}\) = \(\frac{\mathrm{BE}}{\mathrm{EC}}\) … … (i) Thales’ theorem
In ΔABP, DC || AP
∴ \(\frac{\mathrm{BD}}{\mathrm{DA}}\) = \(\frac{\mathrm{BC}}{\mathrm{CP}}\) … … (ii) … [Thales’ theorem
∴ From (i) and (ii),\(\frac{\mathrm{BE}}{\mathrm{EC}}\) = \(\frac{\mathrm{BC}}{\mathrm{CP}}\) (Hence proved)
Or
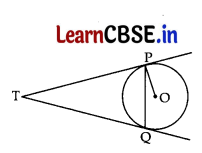
We are given a circle with centre O, an external point T and two tangents TP and TQ to the circle, where P, Q are the points of contact (see Figure).
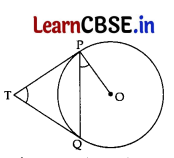
We need to prove that:
∠PTQ = 2∠OPQ
Let ∠PTQ = θ
Now, TP = TQ [∵ Lengths of tangents drawn from an external pt. to a circle are equal
So, TPQ is an isosceles triangle.
∴ ∠TPQ = ∠TQP – \(\frac{1}{2}\) (180° – θ)
= 90° – \(\frac{1}{2}\) θ …………. (i)
Also, ∠OPT = 90° … [∵ Tangent at any point of a circle is ⊥ to the radius through the pt. of contact
So, ∠OPQ = ∠OPT – ∠TPQ
= 90° – (90° – \(\frac{1}{2}\) θ) … [From (i)
∠OPQ =\(\frac{1}{2}\) θ ⇒∠OPQ = \(\frac{1}{2}\) ∠PTQ
∴ ∠PTQ = 2∠OPQ ….(Proved)
Question 23.
The rod AC of a TV disc antenna is fixed at right angle to the wall AB and a rod CD is supporting the disc as shown in Fig., If AC = 1.5 m long and CD = 3 m, find (i) tan θ (ii) sec θ + cosec θ.
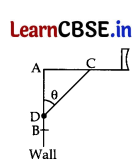
Answer:
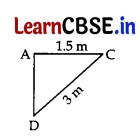
We have, AC = 1.5 m and CD = 3 m
In rt. ∆DAC, sin θ = \(\frac{\mathrm{AC}}{\mathrm{CD}}\)
sin θ = \(\frac{1.5}{3}\)
sin θ = \(\frac{1}{2}\) = sin 30° ….[∵ sin 30° = 1/2
∴ θ = 30°
(i) tan θ = tan 30° = \(\frac{1}{\sqrt{3}}\)
(ii) sec θ + cosec θ = sec 30° + cosec 30°
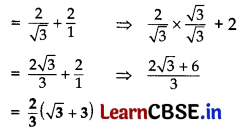
![]()
Question 24.
A piece of wire 22 cm long is bent into the form of an arc of a circle subtending an angle of 60° at its centre. Find the radius of the circle. [Use π = \(\frac{22}{7}\)]
Answer:
Length of the arc = 22 cm
\(\frac{\theta}{180^{\circ}}\) πr = 22
\(\frac{60^{\circ}}{180^{\circ}}\) × \(\frac{22}{7}\) × r = 22
r = \(\frac{22 \times 7 \times 3}{22}\)
∴ r (radius of circle wire) = 21 cm
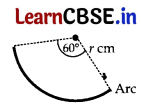
Question 25.
If a number x is chosen at random from the numbers -3, -2, -1, 0, 1, 2, 3. What is the probability that x2 ≤ 4?
Answer:
x : 3, -2, -1, 0, 1, 2, 3, i.e., 7 (seven)
x2 : 9,4,1, 0,1, 4, 9
x2 ≤ 4 : Numbers are 4, 1, 0, 1, 4 i.e., five

∴ P(x2 ≤ 4) = \(\frac{5}{7}\)
Question 26.
Find the mean of the following distribution:

Or
Find the mode of the following data:

Answer:
| Class | Frequency (fi) | xi | fixi |
| 3 – 5 | 5 | 4 | 20 |
| 5 – 7 | 10 | 6 | 60 |
| 7 – 9 | 10 | 8 | 80 |
| 9 – 11 | 7 | 10 | 70 |
| 11 – 13 | 8 | 12 | 96 |
| Σfi = 40 | Σfixi = 326 |
∴ Mean \((\overline{\mathbf{X}})=\frac{\Sigma f_i x_i}{\Sigma f_i}\) = \(\frac{326}{40}\) = 8.15
Or
| Class | Frequency |
| 0 – 20 | 6 |
| 20 – 40 | 8 |
| 40 – 60 | 10 (f0) |
| 60 – 80 | 12 (f1) |
| 80 – 100 | 6 (f2) |
| 100 – 120 | 5 |
| 120 – 140 | 3 |
Since maximum frequency is 12,
∴ Modal class is 60 – 80.
As we know, Mode = l + \(\frac{f_1-f_0}{2 f_1-f_0-f_2}\) × h [∵ l = 60; f0 = 10; f1 = 12; f2 = 6; h = 20
∴ Mode = 60 + \(\frac{12-10}{24-10-6}\) × 20
=60 + (\(\frac{2}{8}\) × 20)
∴ Mode 60 + 5 = 565
Section – C
Questions number 27 to 34 carry 3 marks each.
Question 27.
Find a quadratic polynomial whose zeroes are reciprocals of the zeroes of the polynomial f(x) = ax2 + bx + c, a ≠ 0, c ≠ 0.
Answer:
f(x) = ax2 + bx + c, a ≠ 0, c ≠ 0
Here ‘a’ = a, ‘b’ = b, ‘c’ = c
Let α and β be the zeroes of f(x).
α + β = \(\frac{-b}{a}\) and αβ = \(\frac{c}{a}\)
Then \(\frac{1}{\alpha}\) and \(\frac{1}{\beta}\) are the zeroes of the required polynomial.

= k(cx2 + bx + a) …[where k is any non-zero real number
Question 28.
Not in Current Syllabus.
Answer:
Not in Current Syllabus.
Question 29.
In a flight of 600 km, an aircraft was slowed due to bad weather. Its average speed for the trip was reduced by 200 km/hr and time of flight increased by 30 minutes. Find the original duration of flight.
Answer:
Let the normal speed of the aircraft be x km/hr.
Then the reduced speed of the aircraft = (x – 200) km/hr.
Distance = 600 km (Given)
According to question,

⇒ x(x – 200) = 120000 × 2
⇒ x2 – 200x – 240000 = 0
⇒ x2 – 600x + 400x – 240000 = 0
⇒ x(x – 600) + 400(x – 600) = 0
⇒ (x – 600) (x + 400) = 0
⇒ x – 600 = 0 or x + 400 = 0
⇒ x = 600 or x = -400 …[Speed of an aircraft can not be -ve.
Therefore, Normal speed of the aircraft = 600 km/hr.
Now, Original duration of flight
\(\frac{\text { Distance }}{\text { Speed }}=\frac{600}{600}\) km/hr- = 1 hour
![]()
Question 30.
If the point C(-1, 2) divides internally the line segment joining A(2, 5) and B(x, y) in the ratio 3 :4, find the coordinates of B. A
Answer:
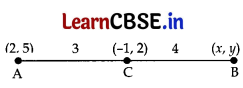
AC : CB = 3 : 4 …[Given
Coordinates of C = Coordinates of C
(-1, 2) (\(\frac{3 x+8}{3+4}, \frac{3 y+20}{3+4}\)) ..[using section formula
\(\frac{3 x+8}{7}\) = -1
3x + 8 = -7
3x = -7 – 8
∴ x = \(\frac{-15}{3}\) = -5
\(\frac{3 y+20}{7}\) = 2
3y + 20 = 14
3y = 14 – 20
∴ y = \(\frac{-6}{3}\) = -2
∴ Point B(x, y) = B(-5, -2)
Question 31.
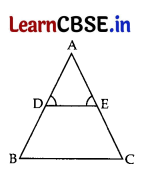
In Fig., ∠D = ∠E and \(\frac{\mathrm{AD}}{\mathrm{DB}}\) = \(\frac{\mathrm{AE}}{\mathrm{EC}}\), prove that BAC is an isosceles triangle.
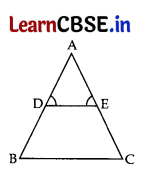
Answer:
In ΔADE, ∠D = ∠E …[Given
AD = AE …. (i)
…[sides opposite to equal angles are equal
\(\frac{\mathrm{AD}}{\mathrm{DB}}\) = \(\frac{\mathrm{AE}}{\mathrm{EC}}\) …[Given
\(\frac{\mathrm{AD}}{\mathrm{DB}}\) =\(\frac{\mathrm{AD}}{\mathrm{EC}}\) …[From (i)
∴ DB = EC
Adding (i) and (ii),
AD + DB = AE + EC
∴ AB = AC
∴ ΔBAC is an isosceles triangle.
Question 32.
Not in Current Syllabus.
Answer:
Not in Current Syllabus.
Question 33.
If sin θ + cos θ = √3, then prove that tan θ + cot θ = 1.
Answer:
We have, sin θ + cos θ = √3
(sin θ + cos θ)2 = (√3)2 …[squaring both sides
⇒ sin2 θ + cos2 θ + 2 sin θ cos θ = 3
⇒ 1 + 2 sin θ cos θ = 3 [∵ sin2 θ + cos2 θ = 1
⇒ 2 sin θ cos θ = 3 – 1
⇒ sin θ cos θ = \(\frac{2}{2}\) = 1 ……….(i)
Now, L.H.S. = tan θ + cot θ
= \(\frac{\sin \theta}{\cos \theta}+\frac{\cos \theta}{\sin \theta}\)
= \(\frac{\sin ^2 \theta+\cos ^2 \theta}{\cos \theta \sin \theta}\) = \(\frac{1}{\cos \theta \sin \theta}\)
= \(\frac{1}{1}\) … [From (i)
= 1 = RHS (Hence Proved)
Question 34.
Not in Current Syllabus.
Answer:
Not in Current Syllabus.
Section – D
Questions number 35 to 40 carry 4 marks each.
Question 35.
Not in Current Syllabus.
Answer:
Not in Current Syllabus.
Question 36.
The sum of four consecutive numbers in AP is 32 and the ratio of the product of the first and last terms to the product of two middle terms is 7 : 15. Find the numbers.
Or
Question 36.
Solve: 1 + 4 + 7 + 10 + … + x = 287
Answer:
Let 4 consecutive numbers in AP be
a – 3d, a – d, a + d, a + 3d
As per the question,
a – 3d + a – d + a + d + a + 3d = 32
⇒ 4a = 32 a = \(\frac{32}{4}\) = 8
Now, \(\frac{(a-3 d)(a+3 d)}{(a-d)(a+d)}\) = \(\frac{7}{15}\)
⇒ \(\frac{a^2-9 d^2}{a^2-d^2}\) = \(\frac{7}{15}\)
⇒ \(\frac{64-9 d^2}{64-d^2}\) = \(\frac{7}{15}\) .. [∵ a = 8
⇒ 448 – 7d2 = 960 – 135d2
⇒ 135d2 – 7d2 = 960 – 448
⇒ 128d2 = 512
⇒ d2 = \(\frac{512}{128}\)
⇒ d2 = 4 ⇒ d = ±2
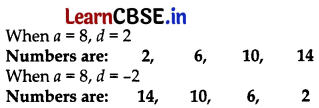
Or
Here 1st term, a = 1 and Common difference, d = 7 – 4 = 4 – 1 = 3
Sn = 287 …[Given
⇒ \(\frac{n}{2}\) [2a + (n – 1)d] = 287
⇒ n[2(1) + (n – 1)3] = 574
⇒ n(2 + 3n – 3) = 574
⇒ n(3n – 1) = 574
⇒ 3n2 – n – 574 = 0
⇒ 3n2 – 42n + 41n – 574 = 0
⇒ 3n(n – 14) + 41(n – 14) = 0
⇒ (n – 14) (3n + 41) = 0
⇒ n – 14 = 0 or 3n + 41 = 0
⇒ n = 14 or n = \(\frac{-41}{3}\) …[not possible as n is a natural number
∴ n = 14 i.e. x is the 14th term.
Now, x = an = a14 = a + 13d = 1 + 13(3)
∴ x = 1+39 = 40
![]()
Question 37.
Not in Current Syllabus.
Answer:
Not in Current Syllabus.
Question 38.
A vertical tower stands on a horizontal plane and is surmounted by a vertical flag-staff of height 6 m. At a point on the plane, the angle of elevation of the bottom and top of the flag¬staff are 30° and 45° respectively. Find the height of the tower. (Take √ 3 = 1.73)
Answer:
Let BC be the tower and CD be the flagstaff.

Question 39.
Not in Current Syllabus.
Answer:
Not in Current Syllabus.
Question 40.
The following table gives production yield per hectare (in quintals) of wheat of 100 farms of a village.

Change the distribution to ‘a more than’ type distribution.
Or
Question 40.
The median of the following data is 525. Find the values of x and y, if total frequency is 100:

Answer:
| Production | No. of farms | c.f | Points | |
| Yield/hect. | 4 | More than or equal to 40 | 100 | (40, 100) |
| 40 – 45 | 6 | More than or equal to 45 | 96 | (45, 96) |
| 45 – 50 | 16 | More than or equal to 50 | 90 | (50, 90) |
| 50 – 55 | 20 | More than or equal to 55 | 74 | (55, 74) |
| 55 – 60 | 30 | More than or equal to 60 | 54 | (60, 54) |
| 60 – 65 | 24 | More than or equal to 65 | 24 | (65, 24) |
Or
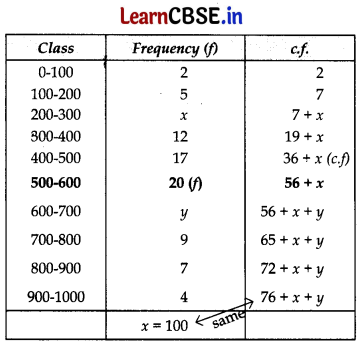
Here, 76 + x + y = 100
⇒ y = 100 – 76 – x = 24 – x ……(i)
Now, \(\frac{n}{2}\) = \(\frac{100}{2}\) = 50 that lies in median class 500 – 600.
Median = 525 …[Given
∴ Median l + \(\frac{\frac{n}{2}-c . f .}{f}\) × h …[f = 20; c.f. = 36 + x; h = 100
⇒ 525 = 500 + [\(\frac{[50-(36+x)]}{20}\) × 100]
⇒ 525 – 500 = (50 – 36 – x) 5
⇒ \(\frac{25}{5}\) = 14 – x ⇒ x = 14 – 5 = 9
Putting the value of x in (i), y = 24 – 9 = 15
∴ x = 9 and y = 15
![]()
SET II Code No. 30/1/2
Note: Except for the following questions, all the remaining questions have been asked in Set – I.
Question 20.
A die is thrown once. What is the probability of getting an even prime number?
Answer:
S = 1, 2, 3, 4, 5, 6 i.e., six.
Even prime number is 2 i.e. one.
∴ P(even prime number) = \(\frac{1}{2}\)
Question 25.
Find the sum of first 20 terms of the following AP: 1, 4, 7,10,…
Answer:
Here 1st term, a = 1 and, common difference, d = 7 – 4 = 4 – 1 = 3
As we know, Sn = \(\frac{n}{2}\)[2a + (n – 1)d]
∴ S20 = \(\frac{20}{2}\) [2(1) + (20 – 1)(3)]
= 10(2 + 57) = 590
Question 26.
The perimeter of a sector of a circle of radius 5.2 cm is 16.4. Find the area of the sector.
Answer:
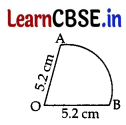
Let the radius of circle, r = 5.2 cm
Perimeter of the sector of a circle = 16.4 cm
⇒ OA(r) + OB(r) + length of arc \(\widehat{\mathrm{AB}}\) = 16.4
⇒ 5.2 + 5.2 + l = 16.4
⇒ l = 16.4 – 5.2 – 5.2 = 6 cm
∴ Area of the sector = \(\frac{n}{2}\)lr
= \(\frac{1}{2}\) × 6 × 5.2 = 15.6 cm2
Question 32.
A train covers a distance of 480 km at a uniform speed. If the speed had been 8 km/h less, then it would have taken 3 hours more to cover the same distance. Find the original speed of the train.
Answer:
Let the original speed of the train be x km/hr. and then the reduced speed of the tain be (x – 8) km/ hr.
Distance = 480 km …[Given
According to Question,
⇒ \(\frac{480}{x-8}-\frac{480}{x}\) = 3 [∴ Time = \(\frac{\text { Distance }}{\text { Speed }}\)
⇒ \(\frac{480[x-(x-8)]}{(x-8)(x)}\)
⇒ x(x – 8) = 1280
⇒ x2 – 8x – 1280 = 0
⇒ x2 – 40x + 32x – 1280 = 0
⇒ x(x – 40) + 32(x – 40) = 0
⇒ (x – 40) (x + 32) = 0
⇒ x – 40 = 0 or x + 32 = 0
x = 40 or x = – 32
(Speed can not be -ve)
∴ The original speed of the train = 40 km/hr.
Question 33.
Prove that the parallelogram circumscribing a circle is a rhombus.
Answer:
Given. ABCD is a ||gm.
To prove. ABCD is a rhombus.
Proof. In ||gm, opposite sides are equal
AB = CD
and AD = BC ………….. (i)
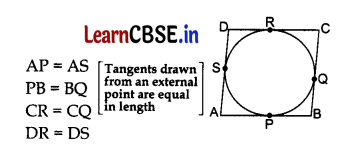
By adding these tangents,
(AP + PB) + (CR + DR) = AS + BQ + CQ + DS
AB + CD = (AS + DS) + (BQ + CQ)
AB + CD = AD + BC
AB + AB = BC + BC …[From (i)
2 AB = 2 BC
AB = BC …….. (ii)
From (i) and (ii), AB = BC = CD = DA
∴ ||gm ABCD is a rhombus.
Question 34.
Prove that: 2(sin6 θ + cos6 θ) -3(sin4 θ + cos4 θ) + 1 = 0.
Answer:

![]()
SET III Code No. 30/1/3
Note: Except for the following questions, all the remaining questions have been asked in Set – I & Set – II.
Question 14.
A ladder 10 m long reaches a window 8 m above the ground. The distance of the foot of the ladder from the base of the wall is ………….. m.
Answer:
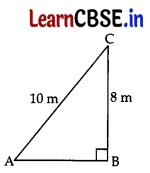
Let AC be the ladder.
In rt. ΔABC,
AB2 + BC2 = AC2 …[Pythagoras’ theorem
AB2 + (8)2 = (10)2
AB2 + 64 = 100
AB2 = 100 – 64 = 36
∴ AB = 6 m
Question 20.
A pair of dice is thrown once. What is the probability of getting a doublet?
Answer:
Two dice can be thrown in 6 × 6 = 36 ways.
‘a doublet’ can be obtained as (1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6) i.e. 6 ways.
∴ P(a doublet) = \(\frac{6}{36}\) = \(\frac{1}{6}\)
Question 25.
The minute hand of a clock is 12 cm long. Find the area of the face of the clock described by the minute hand in 35 minutes.
Answer:
Here an angle obtained in 35 minutes
(θ ) = \(\frac{360^{\circ}}{60^{\circ}}\) × 35 = 210° and r(radius) = 12 cm.
Area of the Sector = \(\frac{\theta}{360}\) r2
= \(\frac{210^{\circ}}{360^{\circ}}\) × \(\frac{22}{7}\) × 12 × 12
= 264 cm2
Therefore, 264 cm2 is the area of the face of the clock described by the minute hand in 35 minutes.
Question 26.
The sum of the first 7 terms of an AP is 63 and that of its next 7 terms is 161. Find the AP.
Answer:
As we know, Sn = \(\frac{n}{2}\)[(2a + (n – 1)d]
S7 = 63 …..[Given
⇒ \(\frac{7}{2}\)[2a + (7 – 1)d] = 63
⇒ \(\frac{1}{2}\)(2a + 6d) = 9
⇒ a + 3d = 9
⇒ a = 9 – 3d …. (i)
S14 – S7 = 161 …[Given
S14 – 63 = 161
S14 = 161 + 63
\(\frac{14}{2}\) [2a + 13d] = 224
2(9 – 3d) + 13d = \(\frac{224}{7}\) …[From (i)
18 – 6d + 13d = 32
7d = 32 – 18
7d = 14
d = \(\frac{14}{7}\) = 2
Putting the value of d in (i), a = 9 – 3(2)
= 9 – 6 = 3
The A.P. is a, a + d, a + 2d, a + 3d, …………….. 3, 5, 7, 9,…
Question 32.
A man can row a boat downstream 20 km in 2 hours and upstream 4 km in 2 hours. Find his speed of rowing in still water. Also find the speed of the stream.
Answer:
(i) Let the speed of boat in still water be x km/hr and the speed of the stream be y km/hr.
Then the speed of the boat downstream = (x + y) km/hr
and speed of the boat upstream = (x – y) km/hr.
As we know, Time = \(\frac{\text { Distance }}{\text { Speed }}\)
According to Question,
Downstream, \(\frac{20}{x+y}\) = 2
⇒ 2(x + y) = 20
⇒ x + y = 10 ………… (i)
Upstream, \(\frac{4}{(x-y)}\) = 2
⇒ 2(x – y) = 4
⇒ x – y = 2 ………… (ii)
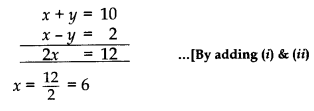
Putting the value of x in (i), y = 4
∴ Speed of boat in still water = 6 km/hr.
and speed of the stream = 4 km/hr.
![]()
Question 33.
In given Fig., two circles touch each other at the point C. Prove that the common tangent to the circles at C, bisects the common tangent at P and Q.
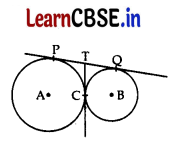
Answer:
To prove: PT = TQ
Proof: PT = TC ……. (i) [Tangents from an external point are equal
TQ = TC …….. (ii)
From (i) & (it), PT = TQ (Hence Proved)
Question 34.
Prove that: \(\frac{\cot \theta+{cosec} \theta-1}{\cot \theta-{cosec} \theta+1}=\frac{1+\cos \theta}{\sin \theta}\)
Answer:

Question 40.
From the top of a 7 m high building the angle of elevation of the top of a tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower.
Answer:
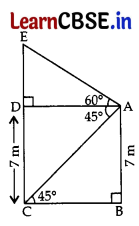
Let AB = 7 m be the building and EC be the tower. Draw AD || BC
In rt. ΔABC,
tan 45° = \(\frac{\mathrm{AB}}{\mathrm{BC}}\)
1 = \(\frac{7}{B C}\)
⇒ BC = 7m ………. (i)
∴ DA = BC = 7 m ….[opposite sides of a square
In rt. ΔADE, tan 60° = \(\frac{\mathrm{DE}}{\mathrm{AD}}\)
√3 = \(\frac{DE}{7}\) ⇒ DE = 7√3 ……(ii)
∴ Height (tower), CE
= CD + DE
= 7(1 + √3)m = 7(1 + 1.73)
= 7(2.73) = 19.11 m