Areas Related to Circles Formulas CBSE Class 10 Maths

Areas Related to Circles Formulas CBSE Class 10 Maths

Circumference of a Circle or Perimeter of a Circle

• The distance around the circle or the length of a circle is called its circumference or perimeter.
• Circumference (perimeter) of a circle = πd or 2πr,
  where d is a diameter and r is a radius of the circle and π = \(\frac { 22 }{ 7 }\)
• Area of a circle = πr²
• Area of a semicircle = \(\frac { 1 }{ 2 }\) πr²
• Area of quadrant = \(\frac { 1 }{ 4 }\) πr²

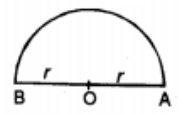
Perimeter of a semicircle:
Perimeter of a semicircle or protractor = πr + 2r

Area of the ring Formulas :
Area of the ring or an annulus = πR² – πr²
= π(R² – r²)
= π (R + r) (R – r)

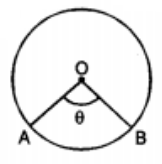
Length of the arc AB = \(\frac { 2\pi r\theta }{ { 360 }^{ 0 } }\) = \(\frac { \pi r\theta }{ { 180 }^{ 0 } }\)

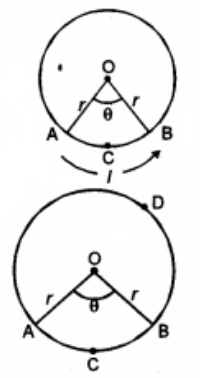
Area of sector formula:

• Area of sector OACBO = \(\frac { \pi { r }^{ 2 }\theta }{ { 360 }^{ 0 } }\)
• Area of sector OACBO = \(\frac { 1 }{ 2 }\) (r × l).

Perimeter of a sector Formula:

Perimeter of sector OACBO = Length of arc AB + 2r
= \(\frac { \pi r\theta }{ { 180 }^{ 0 } }\) + 2r

Other important formulae:

• Distance moved by a wheel in 1 revolution = Circumference of the wheel.
• Number of revolutions in one minute = \(\frac { Distance moved in 1 minute }{ Circumference }\)
• Angle described by minute hand in 60 minutes = 360°
• Angle described by hour hand in 12 hours = 360°
• The mid-point of the hypotenuse of a right triangle is equidistant from the vertices of the triangle.
• The angle subtended at the circumference by a diameter is always a right angle.

Area of a segment Formula Class 10 :

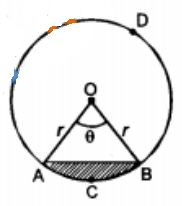
• Area of minor segment ACBA = Area of sector OACBO – Area of ΔOAB
  = \(\frac { \pi { r }^{ 2 }\theta }{ { 360 }^{ 0 } } -\frac { 1 }{ 2 } { r }^{ 2 }sin\theta\)
• Area of major segment BDAB = Area of the circle – Area of minor segment АСВА
  = πr² – Area of minor segment ACBA.
• If a chord subtends a right angle at the centre, then
  Area of the corresponding segment = \(\left( \frac { \pi }{ 4 } -\frac { 1 }{ 2 } \right) { r }^{ 2 }\)
• If a chord subtends an angle of 60° at the centre, then
  Area of the corresponding segment = \(\left( \frac { \pi }{ 3 } -\frac { \surd 3 }{ 2 } \right) { r }^{ 2 }\)
• If a chord subtends an angle of 120° at the centre, then
  Area of the corresponding segment = \(\left( \frac { \pi }{ 3 } -\frac { \surd 3 }{ 4 } \right) { r }^{ 2 }\)

NCERT SolutionsMathsScienceSocialEnglishHindiRD Sharma

• CBSE Board Papers Class 10 Maths Areas Related To Circles
• Areas Related to Circles NCERT Solutions Class 10 Maths VSAQ
• Areas Related to Circles NCERT Solutions Class 10 Maths SAQ 3 Marks
• Areas Related to Circles NCERT Solutions Class 10 Maths SAQ 2 Marks
• Areas Related to Circles NCERT Solutions Class 10 Maths LAQ
• Areas Related to Circles CBSE Class 10 Maths HOTS
• CBSE Class 10 Maths Areas Related to Circles Value Based Questions
• NCERT Exemplar Solutions Class 10 Maths Areas Related to Circles VSAQ
• NCERT Exemplar Solutions Class 10 Maths Areas Related to Circles SAQ
• NCERT Exemplar Solutions Class 10 Maths Areas Related to Circles LAQ
• CBSE Class 10 Maths Areas Related TO Circles Objective Type
• CBSE Class 10 Maths Areas Related to Circles Formative Assessment
• CBSE CCE Summative Assessment Class 10 Maths Areas Related To Circles LAQ
• CBSE CCE Summative Assessment Class 10 Maths Areas Related To Circles SAQ
• CBSE CCE Summative Assessment Class 10 Maths Areas Related To Circles VSAQ