Get Free NCERT Solutions for Class 10 Maths Chapter 1 PDF. Real Numbers Class 10 Maths NCERT Solutions are extremely helpful while doing homework. Ex 1.1 Chapter 1 Class 10 Maths NCERT Solutions were prepared by Experienced LearnCBSE.in Teachers. Detailed answers of all the questions in Chapter 1 maths class 10 Real Numbers Exercise 1.1 provided in NCERT Textbook.
Topics and Sub Topics in Class 10 Maths Chapter 1 Real Numbers:
| Section Name | Topic Name |
| 1 | Real Numbers |
| 1.1 | Introduction |
| 1.2 | Euclid’s Division Lemma |
| 1.3 | The Fundamental Theorem of Arithmetic |
| 1.4 | Revisiting Irrational Numbers |
| 1.5 | Revisiting Rational Numbers and Their Decimal Expansions |
| 1.6 | Summary |
- Class 10 Maths Real Numbers Ex 1.1
- प्रश्नावली 1.1 का हल हिंदी में वास्तविक संख्याएँ
- Class 10 Maths Real Numbers Ex 1.2
- प्रश्नावली 1.2 का हल हिंदी में वास्तविक संख्याएँ
- Class 10 Maths Real Numbers Ex 1.3
- प्रश्नावली 1.3 का हल हिंदी में वास्तविक संख्याएँ
- Class 10 Maths Real Numbers Ex 1.4
- प्रश्नावली 1.4 का हल हिंदी में वास्तविक संख्याएँ
- Real Numbers Class 10 Extra Questions
NCERT Solutions For Class 10 Maths Chapter 1 Real Numbers Ex 1.1
NCERT Solutions for Class 10 Maths Chapter 6 Triangles Ex 1.1 are part of NCERT Solutions for Class 10 Maths. Here we have given NCERT Solutions for Class 10 Maths Chapter 6 Triangles Exercise 1.1
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 10 |
| Subject | Maths |
| Chapter | Chapter 1 |
| Chapter Name | Real Numbers |
| Exercise | Ex 1.1 |
| Number of Questions Solved | 5 |
| Category | NCERT Solutions |
Ex 1.1 Class 10 Maths Question 1.
Use Euclid’s Division Algorithm to find the HCF of:
(i) 135 and 225
(ii) 196 and 38220
(iii) 867 and 255
Solution:

Ex 1.1 Class 10 Maths Question 2.
Show that any positive odd integer is of the form 6q + 1, or 6q + 3, or 6q + 5, where q is some integer.
Solution

Ex 1.1 Class 10 Maths Question 3.
An army contingent of 616 members is to march behind an army band of 32 members in a parade. The two groups are to march in the same number of columns. What is the maximum number of columns in which they can march?
Solution:

Ex 1.1 Class 10 Maths Question 4.
Use Euclid’s division lemma to show that the square of any positive integer is either of the form 3m or 3m + 1 for some integer m.
Solution:

Ex 1.1 Class 10 Maths Question 5.
Use Euclid’s Division Lemma to show that the cube of any positive integer is either of the form 9m, 9m + 1 or 9m + 8.
Solution:
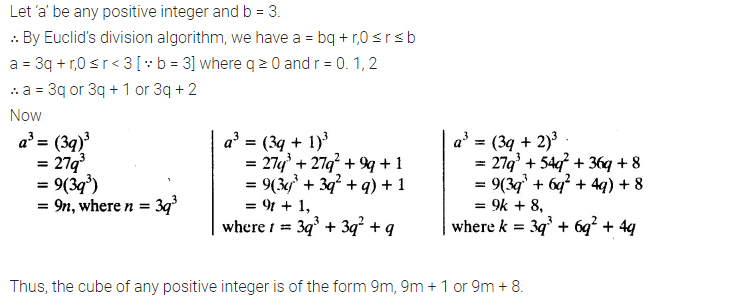
You can also download the free PDF of Class 10 Real Numbers NCERT Solutions or save the solution images and take the print out to keep it handy for your exam preparation.
Real Numbers Class 10 Maths NCERT Solutions PDF Download
Class 10 Maths Real Numbers
Rational numbers and irrational numbers are taken together form the set of real numbers. The set of real numbers is denoted by R. Thus every real number is either a rational number or an irrational number. In either case, it has a non–terminating decimal representation. In the case of rational numbers, the decimal representation is repeating (including repeating zeroes) and if the decimal representation is non–repeating, it is an irrational number. For every real number, there corresponds a unique point on the number line ‘l’ or we may say that every point on the line ‘l’ corresponds to a real number (rational or irrational).
From the above discussion we may conclude that:
To every real number there corresponds a unique point on the number line and conversely, to every point on the number line there corresponds a real number. Thus we see that there is one–to–one correspondence between the real numbers and points on the number line ‘l’, that is why the number line is called the ‘real number line’.
NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers (Hindi Medium) Ex 1.1







Real Numbers Class 10 Maths Objectives
The students will be able to ;
prove Euclid’s Division Lemma
state fundamental theorem of arithmetic
find HCF and LCM using prime factorization
establish the given number as an irrational number
conclude the decimal expansion of a rational number is either terminating or non-terminating repeating.
Chapter 1 Class 10 Maths Real Numbers Summary
We have studied the following points:
1. Euclid’s Division Lemma: Given positive integers a and b, there exist whole numbers q and r satisfying a = bq + r where 0 = r = b.
2. Euclid’s Division Algorithm: According to this, which is based on Euclid’s division lemma, the HCF of any two positive integers a and b with a > b is obtained as follows:
Step 1 Apply the division lemma to find q and r where a = bq + r, O = r < b.
Step 2 If r = 0, the HCF is b . If r? 0 apply Euclid Lemma to b and r
Step 3 Continue the process until the remainder is zero. The divisor at this stage will be HCF (a, b). Also HCF (a, b) = HCF (b, r)
3. The Fundamental Theorem of Arithmetic: Every composite number can be expressed (factorized) as a product of primes and this factorization is unique, apart from the order in which the prime factors occur.
We hope the NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers Ex 1.1, help you. If you have any query regarding Maths NCERT Solutions Chapter 1 Real Numbers Exercise 1.1, drop a comment below and we will get back to you at the earliest.